Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В трапеции ABCD AD||BC, AB = 2 и E – точка пересечения биссектрисы угла BAD
и прямой BC. Окружность, вписанная в треугольник ABE, касается сторон AB и BE
в точках M и H соответственно, MH = 1.
а) Докажите, что MH || AE;
б) Найдите угол BAD



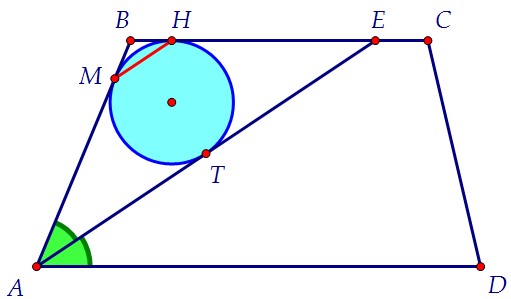Образовавшийся при проведении биссектрисы треугольник АВЕ равнобедренный,
т.к. ∠ЕАD = ∠BEA как внутренние накрест лежащие при параллельных прямых.
Поэтому ∠ВАЕ = ∠ВЕА и выполняется признак равнобедренного треугольника.



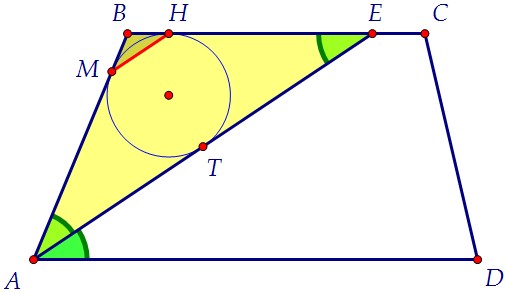Треугольник МВН является равнобедренным по определению, т.к. отрезки
касательных, проведённых из одной точки к окружности, равны (ВМ = ВН).

Равнобедренные треугольники имеют общий угол при вершине, а значит, углы
при основании одного треугольника равны углам при основании другого.

Т.к. ∠ВМН = ∠ВАЕ, а это соответств. углы при прямых МН и АС и секущей АВ,
то прямые MH и AE параллельны по признаку параллельности прямых, ч.т.д.
Доказано заодно и подобие треугольников - они подобны по двум углам.

Чтобы найти ∠BAD, достаточно найти угол при основании равнобедренного
треугольника АВЕ, в который вписана окружность. Обозначим ВМ = х и
воспользуемся равенством отрезков касательных АТ = ЕТ = АМ = 2 - х.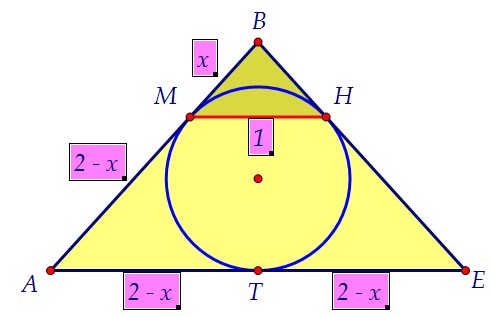



Учитывая подобие, составляем пропорцию:











Итак, равнобедренные треугольники оказались равносторонними.
Поэтому угол ВАЕ равен 60°, а угол ВАD равен 120°.

Ответ: 120°

Автор: Ольга Себедаш             Просмотров: 13469