|
Найдите все действительные значения параметра h, при которых уравнение
x(x + 1)(x + h)(x + h + 1) = h2 имеет ровно четыре действительных корня.
Первые два множителя отличаются на единичку, и последние два - тоже на единичку.
Нули функции f(x) = x(x + 1)(x + h)(x + h + 1) симметричны относит. точки -0,5(h + 1).
***Относительно этой точки попарно симметричны корни: 0 и -h - 1, а также -1 и -h.
Очевидно, что и график функции симметричен относительно прямой x = -0,5(h + 1).
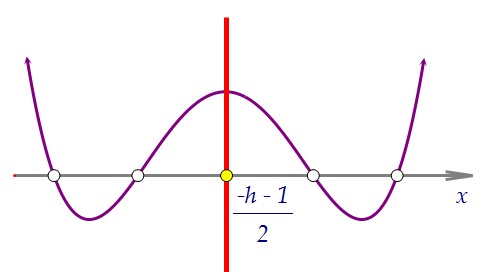Точка x = -0,5(h + 1) является точкой максимума функции, значение в этой точке
неотрицательно. А значения в двух точках минимума равны и неположительны.
Чтобы выполнялось условие задачи, горизонтальная прямая y = h2
должна оказаться строго между минимумом и максимумом функции.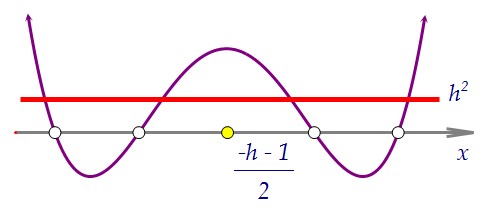
Ниже точки минимума эта прямая оказаться не может, т.к. h2 ≥ 0.
Но значение h = 0 следует проверить отдельно, оно не подойдёт.
Итак, задача сводится к решению следующего неравенства:
.......................................
}>h^2)
.......................................
^2}\cdot{(h-1)^2}}{16}>h^2)
^2}{16}>h^2)
Решения неравенства симметричны относит. h = 0. Пусть h > 0.
^2>16h^2)
Последнее выполняется, если верно одно из неравенств:
 или 
 или 
 или 
Отражая решение относительно нуля, получаем окончательно:
 
========================================
Теперь более подробно о симметричности. Рассмотрим конкретную функцию
f(x) = x(x + 1)(x + 5)(x + 6). Суммы крайних множителей равны (2х + 6).
Множитель, который так и просится в середину произведения, (х + 3).
Корни попарно симметричны относительно точки х = -3.
Сдвинем график на 3 единицы вправо, сделав замену t = х + 3.
Получим f(t) = (t - 3)(t - 2)(t + 2)(t + 3). График этой функции
симметричен относительно оси OY. Ноль - точка максимума.
В исходной задаче делаем аналогичную замену t = х + 0,5(h + 1).
={(t-\frac{h+1}{2})}\cdot{(t-\frac{h-1}{2})}\cdot{(t+\frac{h-1}{2})}\cdot{(t+\frac{h+1}{2})})
Затем находим значение функции в точке максимума:
={(-\frac{h+1}{2})}\cdot{(-\frac{h-1}{2})}\cdot{(\frac{h-1}{2})}\cdot{(\frac{h+1}{2})}=\frac{(h^2-1)^2}{16})
Ну и сводим решение всё к тому же неравенству:
^2}{16}}>h^2)
Автор: Ольга Себедаш Просмотров: 8873
|
