Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найдите все значения параметра a, при которых неравенство х² + 2|х - а| ≥ a²
справедливо для всех действительных x.

Перепишем неравенство таким образом:
х² - a² + 2|х - а| ≥ 0
(х - а)(х + а) + 2|х - а| ≥ 0

При х = а оно выполняется. Хорошо бы, чтобы оно выполнялось и при х > a, и при x < a.

1) Пусть х > a, тогда |х - а| = х - а. Поделим неравенство на х - а > 0. Получим:
х + а + 2 ≥ 0
х ≥ -а - 2



Для выполнения условия потребуем, чтобы
-а - 2 ≤ а
2а ≥ -2
а ≥ -1

2) Пусть х < a, тогда |х - а| = -х + а. Поделим неравенство на х - а < 0. Получим:
х + а - 2 ≤ 0
х ≤ -а + 2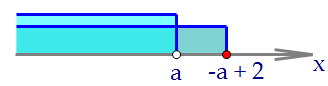



Для выполнения условия потребуем, чтобы
-а + 2 ≥ а
2а ≤ 2
а ≤ 1

Ответ: [-1; 1]

Автор: Ольга Себедаш             Просмотров: 13523