Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

18(C5). ЕГЭ-2014. При каком значении параметра а уравнение (логарифмы) имеет ровно два корня

Найти все значения параметра а, при которых уравнение имеет ровно два решения.
(log₄(x + 2) - log₄(x - 2))² - 11(log₄(x + 2) - log₄(x - 2)) - a² + 3a + 28 = 0

Перед нами квадратное уравнение относительно t, где t = log₄(x + 2) - log₄(x - 2).
Если вы знаете теорему Виета, то корни увидите, проделав некоторые манипуляции.
Если про Виета вам ничего не известно, пропустите их и ищите сразу дискриминант.

t² - 11t - (a² - 3a - 28) = 0
t² - 11t - (a + 4)(a - 7) = 0
t² - 11t + (a + 4)(7 - а) = 0

Итак, корни в любом случае найдены: (a + 4) и (7 - а). Получаем:

$log_4(x + 2) - log_4(x - 2) = a + 4$              $log_4(x + 2) - log_4(x - 2) = 7 - a$

Два получившихся уравнения при x > 2 равносильны следующим:

$log_4{\frac{x+2}{x-2}}=a+4$                                      $log_4{\frac{x+2}{x-2}}=7-a$

=================================================

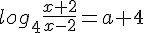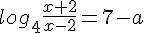Рассмотрим получившуюся дробно-линейную функцию, определённую при x > 2.

$f(x)=\frac{x+2}{x-2}=\frac{x-2+4}{x-2}=1+\frac{4}{x-2}$

Можно сразу заметить, что выражение под знаком логарифма больше единицы,
а значит, само значение логарифма по основанию 5 положительно при x > 2.
Для получения двух корней исходного уравнения достаточно потребовать,
чтобы обе правые части были положительными одновременно:

$\left\{ \begin{array}{rcl} a+4>0\\ 7-a>0 \\ \end{array} \right$

$\left\{ \begin{array}{rcl} a>-4\\ a<7 \\ \end{array} \right$

Прямые совпадают, если a + 4 = 7 - a. Точку а = 1,5 из ответа исключим.

Ответ: (-4; 1,5), (1,5; 7)

=================================================

Можно и продолжить исследование получившейся дробно-линейной функции.

$f(x)=1+\frac{2}{x-2}$

Графиком её является убывающая гипербола с асимптотами x = 2 и y = 1.

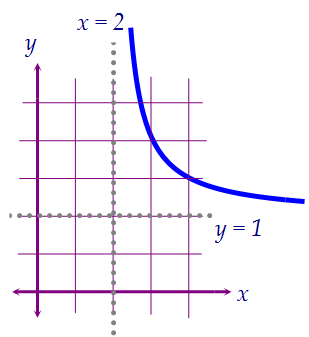C5. ЕГЭ-2014. При каком значении параметра а уравнение (логарифмы) имеет ровно два корня
Совокупность уравнений можно переписать немножко по-другому:

$\frac{x+2}{x-2}=4^{a+4}$                                            $\frac{x+2}{x-2}=4^{7-a}$

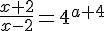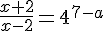Графиками уравнений y = 4^{a + 4} и y = 4^{7 - а} являются горизонтальные прямые.

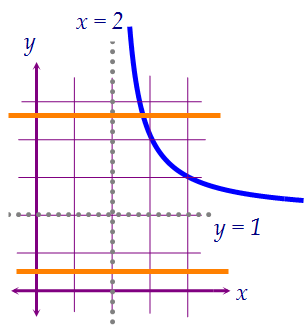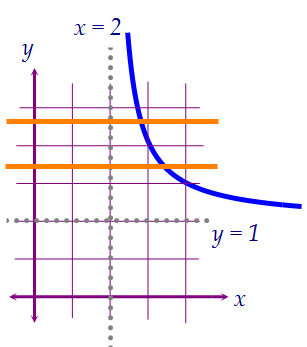C5. ЕГЭ-2014. При каком значении параметра а уравнение (логарифмы) имеет ровно два корня

На рисунках выше прямые пересекают гиперболу в двух точках или не пересекают.
Для выполнения условия задачи обе прямые должны оказаться выше прямой y = 1.
Необходимо ещё не забыть исключить условие совпадения горизонтальных прямых.

=================================================

Осталось решить систему двух уравнений и исключить момент совпадения.

$\left\{ \begin{array}{rcl} 4^{a+4}>1\\ 4^{7-a}>1 \\ \end{array} \right$

$\left\{ \begin{array}{rcl} a>-4\\ a<7 \\ \end{array} \right$

Прямые совпадают, если a + 4 = 7 - a, то есть при а = 1,5. Эту точку из ответа исключим.

Ответ: (-4; 1,5), (1,5; 7)