Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

При каком значении параметра а уравнение имеет ровно два корня?
((|x - 8| + |x - a|)²) - 7a(|x - 8| + |x - a|) + 10a² + 6a - 4 = 0

Заметим, что перед нами квадратное уравнение относительно t, где t = |x - 8| + |x - a|.
Если вы знаете теорему Виета, то корни увидите, проделав некоторые манипуляции.
Если про Виета вам ничего не известно, пропустите их и ищите сразу дискриминант.

t² - 7at + 10a² + 6a - 4 = 0
t² - 7at + 2(5a² + 3a - 2) = 0
t² - 7at + 2(a + 1)(5a - 2) = 0
t² - 7at + (2a + 2)(5a - 2) = 0

Итак, корни в любом случае найдены: (2a + 2) и (5a - 2). Получаем:

|x - 8| + |x - a| = 2a + 2 или |x - 8| + |x - a| = 5a - 2.

=================================================

Рассмотрим функцию f(x) = |x - 8| + |x - a|. Точки 8 и а делят прямую на три области.
На левой области функция убывает (линейная с коэффициентом -2).
На правой области функция возрастает (линейная с коэффициентом 2).
В средней области функция постоянна и неотрицательна, значение её |a - 8|.
(если вы никогда не строили корыто, то постройте его для конкретного значения а).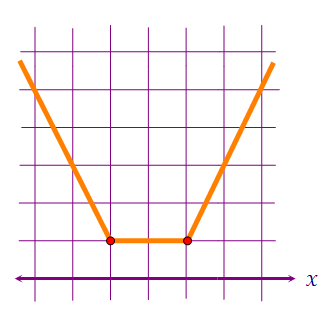



Уравнения y = 2a + 2 и y = 5a - 2 - это уравнения двух горизонтальных прямых.



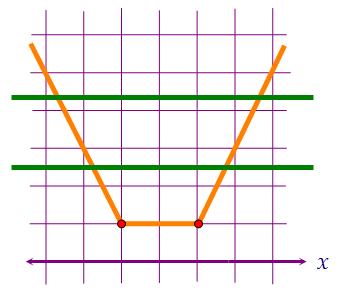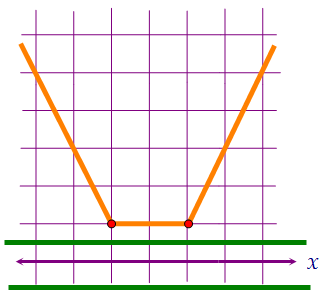На рисунках выше прямые пересекают корыто в четырёх точках или не пересекают.
Ну а чтобы уравнение имело ровно два решения, картинки должны выглядеть так:



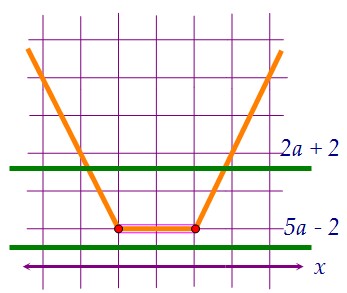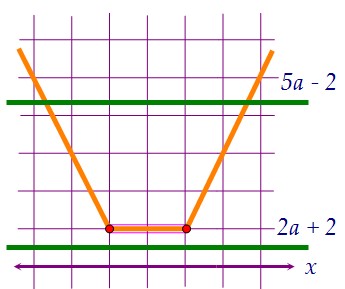Иначе говоря, донышко корыта должно оказаться между горизонтальными прямыми.
Необходимо ещё не забыть проверить условие совпадения горизонтальных прямых.

=================================================

Для достижения цели можно решить две системы строгих неравенств:

                                                     

=================================================

Можно поступить по-другому и решить неравенство методом интервалов:



=================================================

Можно найти, при каких а каждая горизонтальная прямая совпадает
с донышком корыта, решив два простых уравнения с модулем.

|a - 8| = 2a + 2 при а = 2
Если а < 2, то 2a + 2 < |a - 8|
Если а > 2, то 2a + 2 > |a - 8|

|a - 8| = 5a - 2 при а = 5/3
Если а < 5/3, то 5a - 2 < |a - 8|
Если а > 5/3, то 5a - 2 > |a - 8|

2a + 2 < |a - 8| и 5a - 2 > |a - 8| выполняются одновременно при 5/3 < a < 2.
Неравенства 2a + 2 > |a - 8| и 5a - 2 < |a - 8| одновременно не выполняются.

=================================================

Теперь проверим условие, при котором горизонтальные прямые совпадают:

2a + 2 = 5a - 2
а = 4/3

Убеждаемся, что в этом случае обе прямые находятся именно над донышком.

Ответ: 4/3, (5/3, 2)

Автор: Ольга Себедаш             Просмотров: 10726