|
При каких значениях параметра а все числа из отрезка -1 ≤ х ≤ 3удовлетворяют неравенству 2ax + 2√2x + 3 - 2x + 3a - 5 < 0 ?
Заметим несколько выражений (2х + 3) в неравенстве и заменим их на t2.
2ax + 3a - 2x - 3 - 2 + 2√2x + 3 < 0
a(2x + 3) - (2x + 3) - 2 - 2√2x + 3 < 0
at2 - t2 - 2 + 2t < 0
(a - 1)t2 + 2t - 2 < 0 =============================================
Оценим новую переменную t при условии, что -1 ≤ х ≤ 3.
-2 ≤ 2х ≤ 6
1 ≤ 2х + 3 ≤ 9
1 ≤ √2х + 3 ≤ 3
1 ≤ t ≤ 3
=============================================
Один из фокусов данной задачи состоит в том, что если неравенство(a - 1)t2 + 2t - 2 < 0 выполняется для любого t из отрезка [1; 3], то оно выполняется, например, и для t = 1 (удобного нам).Подставив t = 1 в неравенство, получим сразу, что а < 1.Сделаем старший коэффициент неравенства положительным:(1 - а)t2 - 2t + 2 > 0=============================================Если корней у квадратного трёхчлена нет, то неравенство выполняется при любых t ≥ 0, а значит, и при любых t из отрезка [1; 3], что хорошо. Найдём четверть дискриминанта и условие, при котором он отрицателен:1 - 2(1 - а) < 02a - 1 < 0a < 0,5=============================================А если корни есть? Как добиться желаемого? Есть несколько путей.1) Можно расписать условия расположения корней квадратного трёхчлена, используя значения функции на концах отрезка, вершину и дискриминант.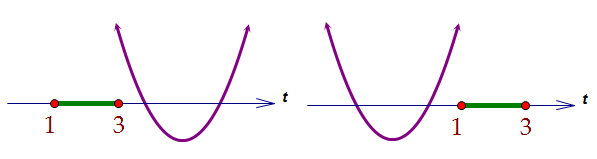 2) Можно найти сами корни трёхчлена через дискриминант и потребовать, чтобы меньший оказался правее трёх или больший - левее единицы.=============================================3) Ну а можно заметить ещё одну хитрость в структуре трёхчлена. Если корни у него есть, то сумма корней равна их произведению. 2) Можно найти сами корни трёхчлена через дискриминант и потребовать, чтобы меньший оказался правее трёх или больший - левее единицы.=============================================3) Ну а можно заметить ещё одну хитрость в структуре трёхчлена. Если корни у него есть, то сумма корней равна их произведению.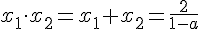 Такое возможно лишь в случае, когда один из корней меньше единицы, а второй корень - больше. Но тогда f(1) < 0, где f(t) = (1 - а)t2 - 2t + 2. Такое возможно лишь в случае, когда один из корней меньше единицы, а второй корень - больше. Но тогда f(1) < 0, где f(t) = (1 - а)t2 - 2t + 2.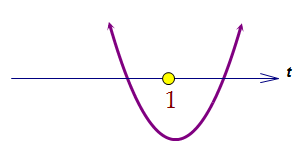 Но было показано, что f(1) > 0. Значит, наличие корней нас не устраивает.Ответ: a < 0,5 Но было показано, что f(1) > 0. Значит, наличие корней нас не устраивает.Ответ: a < 0,5 Автор: Ольга Себедаш Просмотров: 8540
|

 2) Можно найти сами корни трёхчлена через дискриминант и потребовать, чтобы меньший оказался правее трёх или больший - левее единицы.=============================================3) Ну а можно заметить ещё одну хитрость в структуре трёхчлена. Если корни у него есть, то сумма корней равна их произведению.
2) Можно найти сами корни трёхчлена через дискриминант и потребовать, чтобы меньший оказался правее трёх или больший - левее единицы.=============================================3) Ну а можно заметить ещё одну хитрость в структуре трёхчлена. Если корни у него есть, то сумма корней равна их произведению. Но было показано, что f(1) > 0. Значит, наличие корней нас не устраивает.Ответ: a < 0,5
Но было показано, что f(1) > 0. Значит, наличие корней нас не устраивает.Ответ: a < 0,5