Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). На сторонах AD и BC параллелограмма взяты точки
Комментарии к этой задаче: Комментарий добавил(а): Катя Площадь треугольника АРМ в 4 раза больше площади треугольника BPN почему так? объясните по какой формуле мы же не знаем какте у этих треугольников высоты Комментарий добавил(а): Ольга Себедаш Катя, это подобные треугольники. Комментарий добавил(а): Ольга Себедаш "почему АВМ в 2 раза больше ВАN"? Потому что основание одного треугольника в два раза больше другого. А высоты, проведённые к этим основаниям, равны. Комментарий добавил(а): Алина а почему отношение площадей треугольников ABM к BAN равно 2, а не 4? Комментарий добавил(а): Резанова Объясните, пожалуйста,площадь почему АВМ в 2 раза больше ВАN Комментарий добавил(а): Мария Подскажите, почему площадь зелёного треугольника ВЕА в 4 раза больше, чем площадь голубого BEN? Комментарий добавил(а): Ольга Себедаш Мария, потому что основание зелёного в четыре раза больше. А высоты у треугольников одинаковые. Комментарий добавил(а): Любовь Откуда видно, что основание зеленого в четыре раза больше? Про вторую сторону параллелограмма ничего не сказано. Комментарий добавил(а): мария Скажите пожалуйста по каким углам подобны треугольники? (в первом пункте) помимо вертикальных? Комментарий добавил(а): Ольга Себедаш Прямые параллельны, значит по внутренним накрест лежащим углам. Комментарий добавил(а): оля почему площадь зелёного треугольника ВЕА в 4 раза больше, чем площадь голубого BEN. Комментарий добавил(а): Анастасия Здравствуйте, объясните, пожалуйста, почему площади треугольников APT и AMT равны? Комментарий добавил(а): Thomastax Комментарий добавил(а): Комментарий добавил(а): 🙏 Добавить Ваш комментарий: |
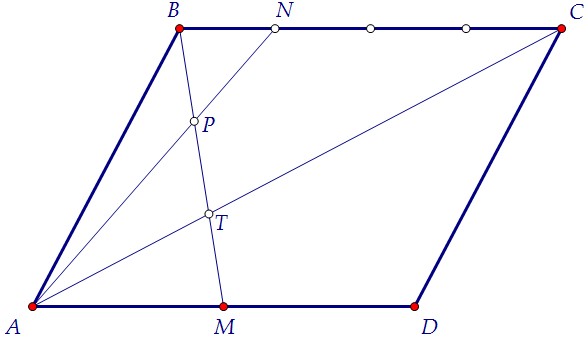Треугольники BPN и MPA подобны по двум углам (докажите).
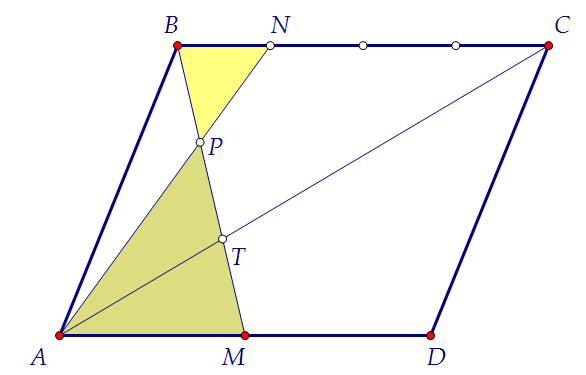BP : PM = BN : AM = 1 : 2. Следовательно, 
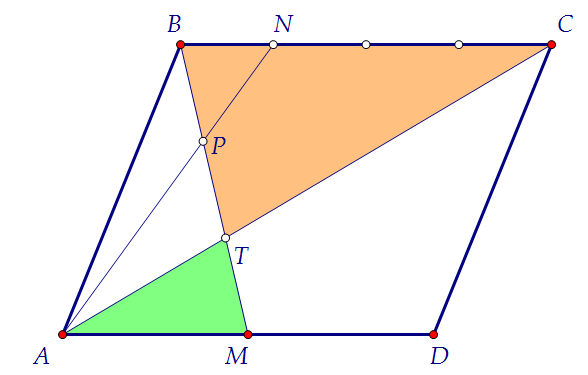MT : BT = AM : BC = 1 : 2. Следовательно, 
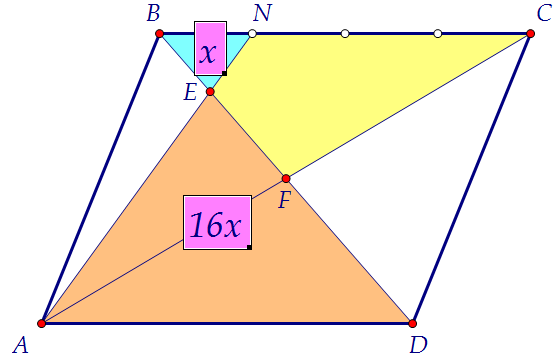Площадь зелёного треугольника ВЕА в 4 раза больше, чем площадь голубого BEN.
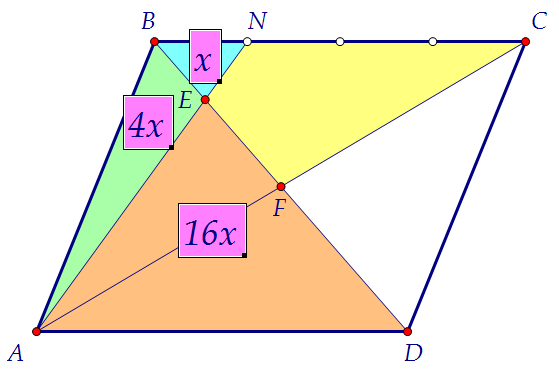Зелёный и рыжий треугольники вместе составляют половину всего параллелограмма.4х + 16х = 520х = 5х = 0,25
Найдём площадь искомого четырёхугольника как разность площадей треугольников:
SENCF = SBFC - SBEN
SENCF = 0,25·SABCD - 0,25
SENCF = 0,25·10 - 0,25
SENCF = 2,5 - 0,25
SENCF = 2,25
Ответ: 2,25=====================================
в) Вернёмся к первой паре подобных треугольников. Отношение их площадей равно квадрату коэффициента подобия, то есть площадь одного в 4 раза
больше площади другого. Обозначим площадь треугольника BPN через х
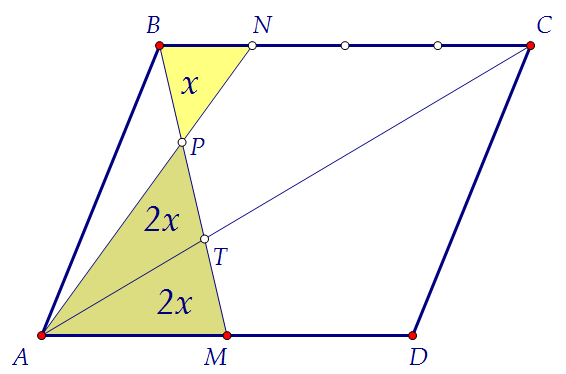У второй пары подобных треугольников отношение площадей тоже равно 4.
Так как площадь маленького равна 2х, то площадь большого равна 8х.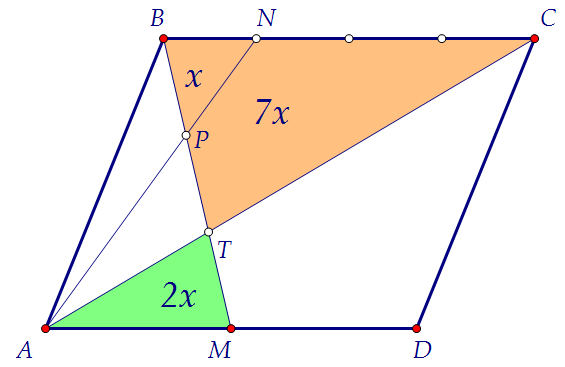
Площадь треугольника АВС составляет половину площади параллелограмма.
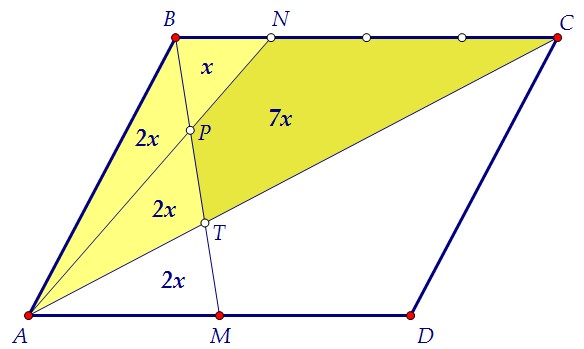12х = 48:212х = 24х = 27х = 14Ответ: 14
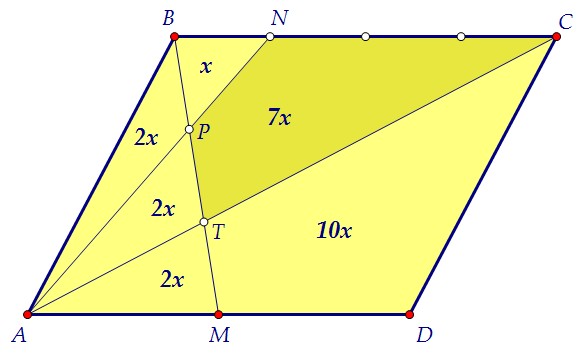Заметьте следующие интересные факты:
--- Площадь треугольника АРМ в 4 раза больше площади треугольника BPN--- Площадь треугольника ВТС в 4 раза больше площади треугольника АТМ--- Площадь треугольника АВМ в 2 раза больше площади треугольника BАN--- Площадь треугольника ANC в 3 раза больше площади треугольника ABN--- AP = 2·PN--- CT = 2·AT