Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). Окружность, вписанная в треугольник, касается средней линии (вар. 63)
Комментарии к этой задаче: Комментарий добавил(а): Римма КРАСИВО! Комментарий добавил(а): Влад Очень классно, Ольга Игоревна! Комментарий добавил(а): Рома Почему сумма боковых сторон треугольника в два раза больше,суммы боковых сторон трапеции Комментарий добавил(а): Ан Рома В задаче написано, что окружность касается средней линии треугольника, то есть DE. А угадай, что средняя линия делает со сторонами треугольника?) Добавить Ваш комментарий: |
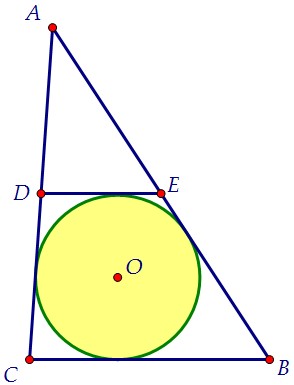
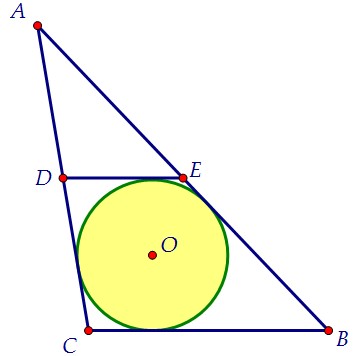Суммы противоположных сторон вписанной трапеции равны: DE + BC = DC + BE. К тому же средняя линия треугольника (а) в два раза меньше основания (2а).
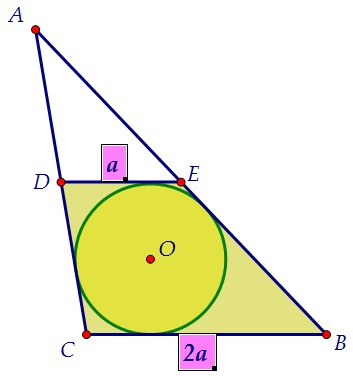Сумма боковых сторон трапеции равна (3а). Сумма боковых сторон треугольника в два раза больше, т.е. равна (6а). АВ + АС = 6а = 3·(2а) = 3·ВС, ч. т. д.===========================================Воспользуемся доказанным и сделаем обозначения сторон треугольника:
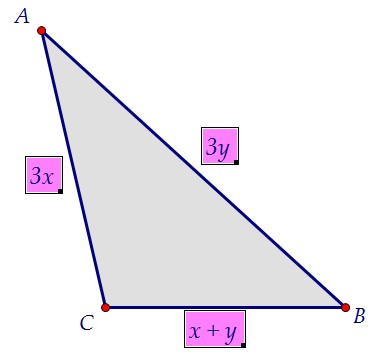Найдём полупериметр треугольника и все составляющие формулы Герона:p = 2x + 2yp - BC = x + yp - AC = 2y - xp - AB = 2x - yS2 = (2x + 2y)(x + y)(2y - x)(2x - y) = 2(x + y)2(2y - x)(2x - y).S2 = 2(x + y)2·m·n.Площадь S и значение (x + y) нам даны, а два последних множителя в сумме дают (x + y). Обозначим их так: m = 2y - x, n = 2x - y.