Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Решите неравенство

Решим неравенство классическим способом, рассмотрев два случая:
1) если х + 2 > 1, то 0 < 2х² + х ≤ (x + 2)²
2) если 0 < х + 2 < 1, то 2х² + х ≥ (x + 2)²
Надо решить две системы и объединить их решения.
======================================
Начнём с первой. Основание логарифма больше единицы.







Можно рассуждать устно. Т.к. х > -1, то х + 1 > 0, и значит, х ≤ 4, т.е. -1 < x ≤ 4.
Из третьего получаем, что х < -0,5 или х > 0. В итоге -1 < x < -0,5 или 0 < x ≤ 4.

Можно и картинку сделать для каждого неравенства: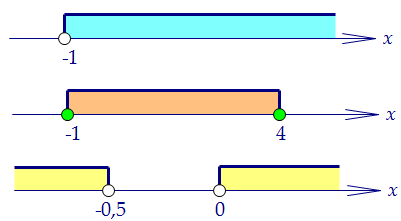



В пересечении получаем два интервала (-1; -0,5) и (0; 4].



======================================
Решим вторую систему. Основание логарифма положительно, но меньше единицы.





Сначала устно. Т.к. х < -1, то х + 1 < 0, и значит, х ≤ 4, т.е. -2 < x < -1.
Картинка для неравенств выглядит так: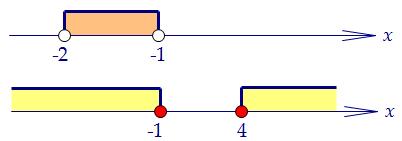



В пересечении получаем интервал (-2; -1).
======================================
Объединяя оба решения, получаем результат:



Ответ: (-2; -1); (-1; -0,5); (0; 4]

======================================
Теперь решим неравенство методом рационализации. Найдём ОДЗ.
Иначе говоря, те значения х, при которых неравенство определено.







Перепишем исходное неравенство так:



На области допустимых значений оно равносильно неравенству:
(х + 2 - 1)(2х² + х - (х + 2)²) ≤ 0
(х + 1)(х² - 3х - 4) ≤ 0
(х + 1)(х + 1)(х - 4) ≤ 0
(х + 1)²(х - 4) ≤ 0
Так как х ≠ -1, то (х + 1)² > 0, а значит, (х - 4) ≤ 0 и х ≤ 4.
Учитывая область допустимых значений, получаем ответ:



Ответ: (-2; -1); (-1; -0,5); (0; 4]

Автор: Ольга Себедаш             Просмотров: 10457