Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Площадь треугольника АВС равна  12. На прямой АС взята точка D так, что
точка C является серединой отрезка AD.  Точка K – середина стороны AB,
прямая KD пересекает сторону BC в точке L.
а) Докажите, что BL : LC = 2 : 1.
б) Найдите площадь треугольника BLK.

Для начала аккуратно сделаем чертёж, помечая по ходу дела равенство отрезков.



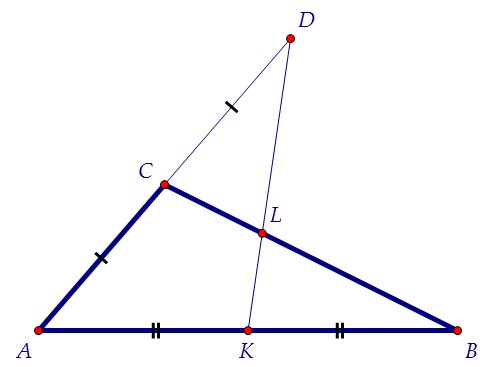Теперь несложно заметить, что соединив точки В и D, мы получим треугольник АВD,
в котором DK и ВС являются медианами по определению (помните ли Вы его?)



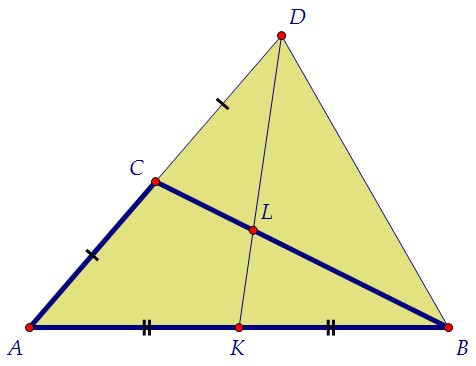А медианы в точке пересечения делятся в отношении 2 : 1, считая от вершины.
Дело сделано. Напишите, умеете ли Вы это свойство доказать самостоятельно?
Найти площадь треугольника BLK можно по-разному. Пусть АЕ - третья медиана



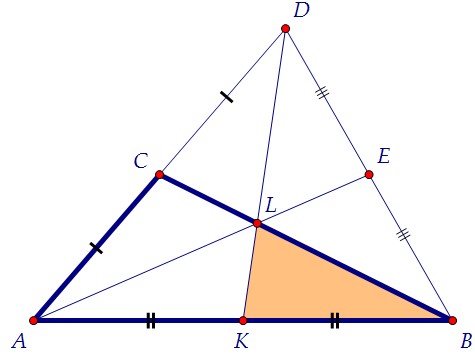треугольника АВD, она пройдёт через точку L пересечения первых двух.
Медиана ВС делит треугольник АВD на два равновеликих треугольника.
Поэтому площадь АВD вдвое больше площади АВС и равна 12·2 = 24.
Три медианы делят треугольник на шесть равновеликих треугольников.
Отсюда легко найти площадь искомого треугольника BLK.   24:6 = 4.
Замечу, что оба эти утверждения следует тоже уметь доказывать.
========================================
Можно сравнить площади треугольников BLK и АВС, не трогая медианы.



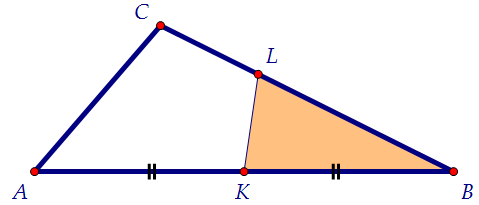Треугольники эти имеют общий угол В, воспользуемся этим фактом.

              

Найдём теперь отношение площадей:



Таким образом, площадь BLK в три раза меньше площади АВС.

Ответ: 4

Автор: Ольга Себедаш             Просмотров: 14056