Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
16(C4). Четыре треугольника, заштрихованные на рисунке, равновелики (вар. 61)
Комментарии к этой задаче: Комментарий добавил(а): Галина Большое спасибо за красивое решение! Гениально! Комментарий добавил(а): училка и мы хотим, чтобы все это решалось за 4 часа Комментарий добавил(а): Ольга Себедаш Раиса, задача сложна именно началом рассуждений. Понять бы, за что браться в первую очередь. Именно поэтому я прошла по лестнице и вверх, и вниз. Если начать сразу с доказательства параллельности, решение будет смотреться фокусом и выглядеть короче. Мне это решение кажется самым простым из всех. Комментарий добавил(а): Раиса Задача сложная и решение далеко не простое.Вряд ли ученикам под силу. Мне интересно Ваше мнение по поводу моего решения(стр.8 форума).Я использовала только равенство пл-дей 4-х тр-ков и отн-е пл.тр.с общей вершиной и основаниями на одной прямой Комментарий добавил(а): Галина Не каждый ребёнок сможет в стрессовой ситуации ЕГЭ так спокойно идти к цели, хотя особых теоретических знаний здесь и не требуется Комментарий добавил(а): Добавить Ваш комментарий: |
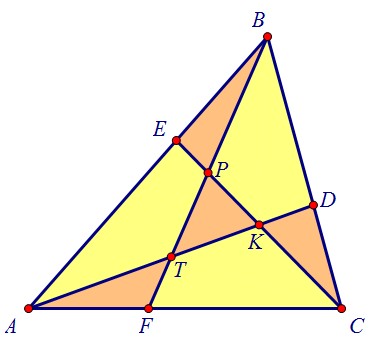
Чтобы доказать, что Р - середина BF, надо бы доказать, что АВР и AFР равновелики.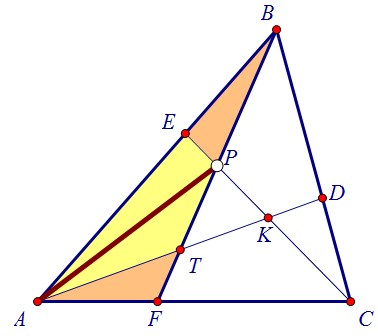
А для этого нужно показать равенство площадей АТР и АЕР. Идём дальше.
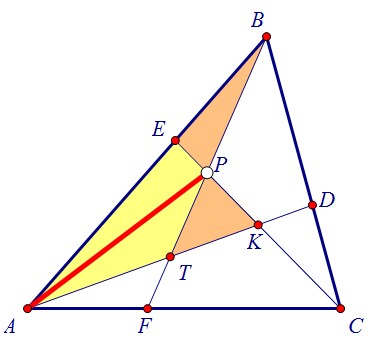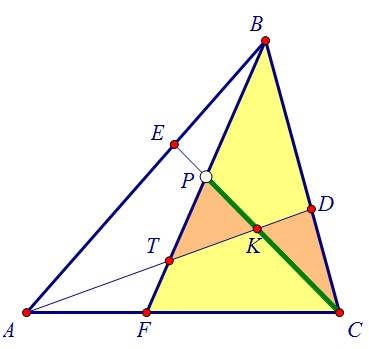
Площади жёлтого и рыжего треугольников относятся, с одной стороны, как АТ:ТК, а с другой, как АЕ:ЕВ. Наша цель - доказать равенство отношений: АТ:ТК = АЕ:ЕВ.Ну а последнее станет очевидным, если будет доказана параллельность ТЕ и КВ.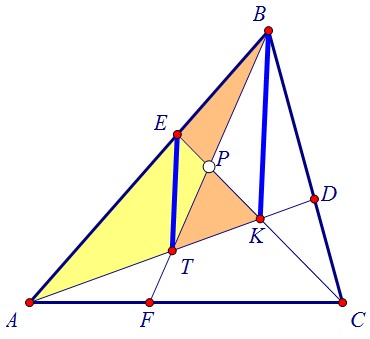
Теперь, когда цель ясна, начнём с доказательства параллельности и пойдём назад.==============================================Т.к. равны площади рыжих треугольников, то равновелики треугольники КТВ и ВЕК.Основание у них общее, а значит, равны расстояния от точек Т и Е до прямой ВК.Итак, ТЕ и КВ параллельны и АТ : ТК = АЕ : ЕВ. Вернёмся к предыдущему рисунку.
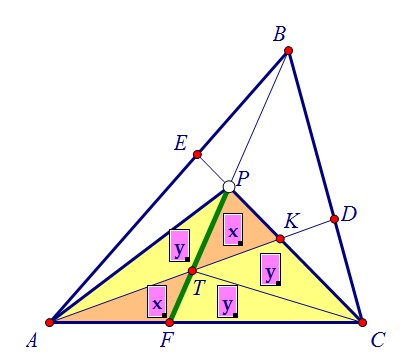Учитывая то, что x : y = FT : TP и y : (x+y) = FT : TP, составим пропорцию: