Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найти все значения параметра а, при каждом из которых уравнение
sin²x + (a - 2)²sinx + a(a - 2)(a - 3) = 0
имеет на отрезке [0; 2π] ровно три корня.

Решать ли квадратное относительно sinx уравнение? Как искать его корни? Искать ли?
Если дискриминант оказался бы покрасивее, то почему бы и нет. Но в нашем случае...
Тогда представим, что квадратное уравнение решено. Какой расклад нас бы устроил?
а) Пусть корни уравнения 0,2 и 0,7. Тогда мы бы стали решать уравнения sinx = 0,7
и sinx = 0,2 и получили бы четыре корня на отрезке [0; 2π]. Не наш вариант.
б) А если корни квадратного уравнения были бы -0,3 и 92? А если 0 и 15? А если...?
Рассуждая таким образом, приходим к программе-минимум:
Один из корней квадратного уравнения равен 1 или -1 или 0. Уже неплохо.
В идеале хотелось бы получить один из трёх вариантов (смотри рисунок).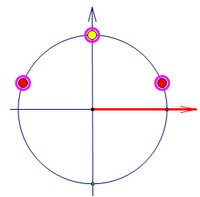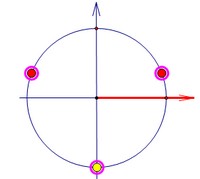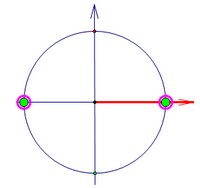



Если Вас смущает последний вариант, пересчитайте корни на отрезке снова.
Теперь подставим вместо sinx в данное уравнение 1 или -1 или 0 по очереди.
1) если sinx = 1, то 1 + (a - 2)² + a(a - 2)(a - 3) = 0
2) если sinx = -1, то 1 - (a - 2)² + a(a - 2)(a - 3) = 0
3) если sinx = 0, то a(a - 2)(a - 3) = 0
=============================================
Прежде чем заняться этими уравнениями, замечу, что даже если мы их решим,
найденные а в ответ сходу записывать нельзя. Это лишь необходимые условия,
которые потребуют проверки. Важен и другой корень квадратного уравнения.
=============================================
Проще всего решается третье уравнение, его корни 0, 2 и 3. Проверим каждый.
---- если а = 2, то sin²x = 0; sinx = 0. Устраивает.
---- если а = 0, то sin²x - 4sinx = 0; sinx = 0. Устраивает.
---- если а = 3, то sin²x - sinx = 0; sinx = 0 и sinx = 1. Не устраивает.
=============================================
Решим второе уравнение. Можно, например, заметить один из его корней (3).
Ну а можно заняться разложением на множители левой части:
1 - (a - 2)² + a(a - 2)(a - 3) = 0
-(а² -4а + 3) + a(a - 2)(a - 3) = 0
-(а - 3)(а - 1) + a(a - 2)(a - 3) = 0
(а - 3)(а² - 2а - а + 1) = 0
(а - 3)(а² - 3а + 1) = 0
                 
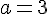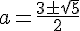Тройку мы уже проверили. Не подставлять же в уравнение радикалы!
Нам нужно, чтобы второй корень оказался строго между числами -1 и 1.
Можно ли его найти, не решая уравнения? Конечно. Поможет т. Виета.
Если первый корень равен -1, то второй корень равен -a(a - 2)(a - 3).

                 

                 

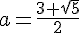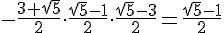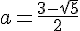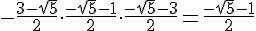Итак, первое значение а нас устраивает, а второе - нет.
=============================================
Первое уравнение 1 + (a - 2)² + a(a - 2)(a - 3) = 0 самое трудное.
Поэтому сразу начнём с его второго корня х₂ = a(a - 2)(a - 3).
Если этот корень (т.е. свободный член) находится между -1 и 1,
то уравнение, очевидно, решений не имеет, т.к. левая часть
строго положительна. Решать уравнение бессмысленно.

Ответ: 0, 2,

Автор: Ольга Себедаш             Просмотров: 11930