Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Постоянно работают курсы для выпускников, учителей и репетиторов

16(C4). Продолжение общей хорды пересекает общую касательную окружностей (вар. 60)

Продолжение общей хорды АВ двух пересекающихся окружностей радиусов 8 и 2
пересекает их общую касательную в точке С, точка А лежит между В и С,
а М и N - точки касания.
а) Докажите, что отношение расстояний от точки С до прямых АМ и AN равно 1:2.
б) Найдите радиус окружности, проходящей через точки А, М и N.

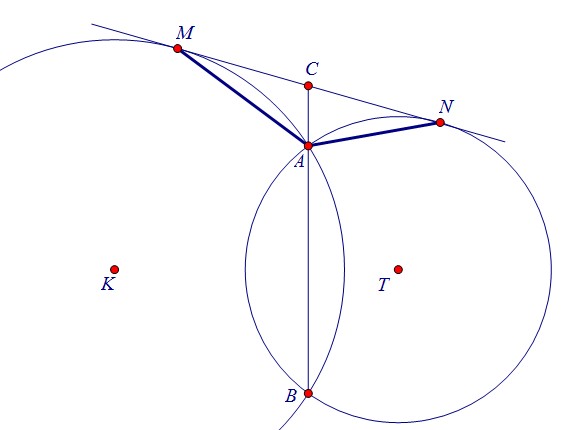Продолжение общей хорды пересекает общую касательную окружностей (вар. 60)

Проанализировав условие, замечаем сразу, что точка С - середина отрезка MN,
т.к. по свойству касательных и секущих, проведённых из точки к окружности
CM² = CA · CB и CN² = CA · CB, и значит, CM = СN.
Из этого тут же следует равенство площадей треугольников МСА и NCA.

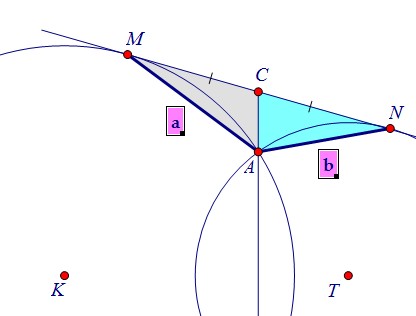C4. Продолжение общей хорды пересекает общую касательную окружностей (вар. 60)

Расстояния от точки С до прямых АМ и AN есть не что иное, как высоты треугольников,
проведённые к сторонам АМ и AN. Произведение этих высот на основания постоянно,
поэтому достаточно найти отношение оснований a:b (доказать, что оно равно двум).

Существенную роль в данной задаче должны сыграть углы ANM (∠α) и AMN (∠β).
Каждый - это угол между хордой и касательной, проведённой через конец хорды.

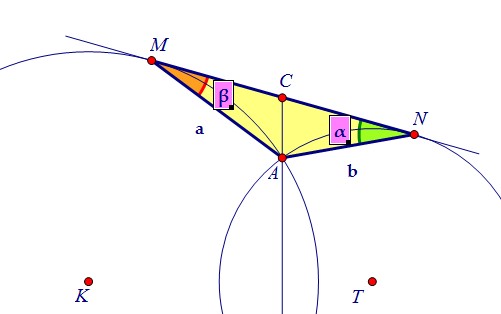C4. Продолжение общей хорды пересекает общую касательную окружностей (вар. 60)

Из теоремы синусов a : sinα = b : sinβ следует равенство a : b = sinα : sinβ.
Чтобы найти отношение синусов, вспомним, что углы между касательной
и хордами AN и AM равны половинам дуг, которые стягивают эти хорды.

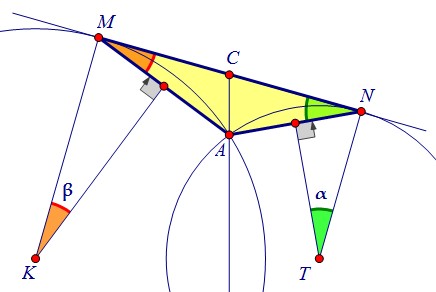C4. Продолжение общей хорды пересекает общую касательную окружностей (вар. 60)

Углы α и β равны половинам центральных углов, опирающихся на хорды.
Проведя из центров окружностей перпендикуляры к отрезкам AN и AM,
получим прямоугольные треугольники с углами α и β соответственно.

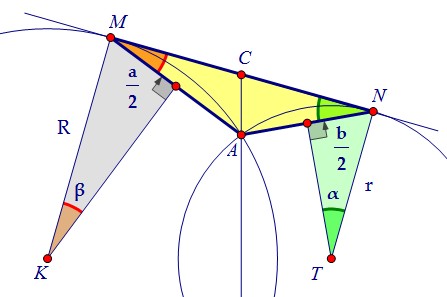C4. Продолжение общей хорды пересекает общую касательную окружностей (вар. 60)

Из треугольников выразим синусы α и β через радиусы окружностей:

$sin{\alpha}=\frac{b}{2r}$                                    $sin{\beta}=\frac{a}{2R}$

Возвращаемся к отношению, полученному из теоремы синусов:

$\frac{a}{b}=\frac{sin{\alpha}}{sin{\beta}}={\frac{b}{2r}}:{\frac{a}{2R}}=\frac{{b}\cdot{R}}{{a}\cdot{r}}={\frac{b}{a}}\cdot{\frac{R}{r}}$

Отсюда следует замечательный вывод:

$\frac{a^2}{b^2}=\frac{R}{r}$                                           $\frac{a}{b}=\sqrt{\frac{R}{r}}=\sqrt{\frac{8}{2}}=\sqrt{4}=2$

Отношение оснований a и b треугольников МСА и NCA равно двум,
значит, отношение соответствующих высот равно 1:2, ч.т.д.
=======================================
Найдём радиус х окружности, описанной около треугольника AMN.

$2x=\frac{a}{sin{\alpha}}$                                     $x=\frac{a}{2sin{\alpha}}$

Подставим в полученное равенство а = 2R·sinβ:

$x=\frac{2Rsin{\beta}}{2sin{\alpha}}=\frac{Rsin{\beta}}{sin{\alpha}}={R}\cdot{\frac{sin{\beta}}{sin{\alpha}}}={R}\cdot{\frac{b}{a}}={8}\cdot{\frac{1}{2}}=4$