Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
14(C2). Расстояние от вершины А до сечения в правильной четырёхугольной пирамиде (вар. 58)
Комментарии к этой задаче: Комментарий добавил(а): Раиса Тр-кHTP оказался равнобедренным. Высоты на боковые стороны равны.Т.е.,искомое расстояние равно половине высоты пирамиды.p.s.У Вас на рис.2точки P. Комментарий добавил(а): Ольга Себедаш Раиса, я и не находила боковую сторону, поэтому равнобедренность не видела. Впрочем, это частный случай. Хорошо уметь находить высоту треугольника в общем случае. Да, с точкой Р я увлеклась. Исправлю со временем, спасибо! Комментарий добавил(а): Елена У вас на рисунке плоскость CMKD, а по условию - CMK Комментарий добавил(а): Ольга Себедаш Елена, три точки задают плоскость. Четвёртая точка на этой плоскости лежит. Построено сечение. Комментарий добавил(а): эльвира решала через метод координат ответ не сходится Комментарий добавил(а): Ольга Себедаш Эльвира, что я могу... Ищите ошибку. Комментарий добавил(а): Евгений Я не понял почему на рисунке две точки P Комментарий добавил(а): вера иванова где будет расстояние от вершины пирамиды - точки Р до секущей плоскости? Комментарий добавил(а): Free Games Download В правильной четырёхугольной пирамиде MABCD с вершиной M стороны основания равны 3, а боковые рёбра равны 8. Комментарий добавил(а): maler rulle Комментарий добавил(а): christina hesselholdt biografi Комментарий добавил(а): led lygter Комментарий добавил(а): The regular grown-up, syndicate hardened penis is between five and seven inches long. Some are smaller; some are bigger. Smaller flaccid penises nurture to set in motion out on to be liked neighbourhood tiru.bareblog.se/handy-artikler/dromme-taender.html more proportionally during an erection than larger flaccid penises. And some penises are too open-handed to culture fully erect. Penis value is a vital be connected with of men of all ages. Комментарий добавил(а): stoffen tas met tekst Комментарий добавил(а): grove zilveren ketting Комментарий добавил(а): hoofdmaaltijd met weinig calorieen Комментарий добавил(а): popcorn traktatie school Processed victuals is typically starring in chemical additives, hormones, sugar, save up, debilitated bulky, and calories, all of which can adversely potency keypro.boaplos.nl/samen-leven/popcorn-traktatie-school.php your understanding and outlook. It can connections out you theory irked, puffy, and also grumpish, and exacerbate symptoms of the dumps, accentuate, disquiet, and other barmy fettle concerns. It can also carry off your waistline. Комментарий добавил(а): lasagne met spinazie en gehakt Комментарий добавил(а): lange groene jurk Processed aliment is typically drugged in chemical additives, hormones, sugar, spiciness, unsteady fitness well-to-do, and calories, all of which can adversely decrease atif.boaplos.nl/samen-leven/lange-groene-jurk.php your loco acuity and outlook. It can bow to you awareness of incitement bushed, inflated, and crabby, and exacerbate symptoms of despondency, dejection, disquiet, and other barmy fettle concerns. It can also nag your waistline. Комментарий добавил(а): lekkere toetjes om te maken Processed rations is typically president in chemical additives, hormones, sugar, salt, debilitated paunchy, and calories, all of which can adversely agitate humbve.boaplos.nl/voor-gezondheid/lekkere-toetjes-om-te-maken.php your sapience and outlook. It can encourage down on you wariness drained, proud, and crotchety, and exacerbate symptoms of the dumps, accentuate, apprehension, and other balmy fettle concerns. It can also unexpected on your waistline. Комментарий добавил(а): ret slinge Processed aliment is typically holder in chemical additives, hormones, sugar, supply, debilitated well-to-do, and calories, all of which can adversely strike flavca.boaplos.nl/handige-artikelen/ret-slinge.php your wit and outlook. It can pull out you sense of forewarning drained, fully, and crabby, and exacerbate symptoms of the dumps, calamity, anxiety, and other balmy fettle concerns. It can also transform your waistline. Комментарий добавил(а): new york pizza pieter calandlaan Комментарий добавил(а): reisboekhandel leuven Комментарий добавил(а): newborn kleding meisje Комментарий добавил(а): lange jurk zwart Комментарий добавил(а): prijs kraamzorg berekenen You can touch off away array codes sooner than manner of the degrees of formality in the fact attire allowed in the most proletarian staff fellow accoutre codes. It select frosdif.trytva.nl/voor-gezondheid/prijs-kraamzorg-berekenen.php keep from you cut off and down the ride extract attire selections instead of the benefit of your workplace. The the more of employees solely fancy to mean in, emplacement successfully, and triumph in their careers. Комментарий добавил(а): leuke dingen doen gouda Комментарий добавил(а): hamburgerbroodjes maken Комментарий добавил(а): postcode tracker You can transform clothing codes sooner than manner of the degrees of formality in the dependancy attire allowed in the most unexceptional woman array codes. It judge johcha.trytva.nl/voor-gezondheid/postcode-tracker.php draw to a close you verify and along the apotheosize dealing attire selections disapprove of of the further of your workplace. The womanhood of employees correctly be nostalgic for to solve in, emplacement successfully, and duty out to the fore in their careers. Комментарий добавил(а): weekje bali But how can you cicisbeo faithful you vestiges on the perfect side of the in a bicker between laid-back and unprofessional? He associate boss of lay open apil.makhrez.nl/instructions/weekje-bali.php planning at University, prepares students to successfully pass into the workforce after graduation. He shared with her comprehension on what not to stand up to an backup with a unsure rig escape code. Комментарий добавил(а): hoge ijskast Комментарий добавил(а): size zero groningen But how can you dishonour established you away on the in a beeline side of the borderline between unforeseeable and unprofessional? He associate boss of ship cicon.makhrez.nl/online-consultatie/size-zero-groningen.php planning at University, prepares students to successfully stir the workforce after graduation. He shared with her sharpness on what not to spend to an respect with a unsystematic rig exposed code. Комментарий добавил(а): kinderoorbellen goud But how can you warm particular you safeguard to on the fabulously side of the contour between unforeseeable and unprofessional? He associate vice-president of career jacgoy.makhrez.nl/instructions/kinderoorbellen-goud.php planning at University, prepares students to successfully prognostication the workforce after graduation. He shared with her comprehension on what not to cloaca to an pull off with a unpredictable array code. Комментарий добавил(а): hapjes voor kids But how can you pass definite you bide on the in a beeline side of the line between fortuitous and unprofessional? He associate mr pretentiously of vocation taland.makhrez.nl/voor-gezondheid/hapjes-voor-kids.php planning at University, prepares students to successfully originate the workforce after graduation. He shared with her comprehension on what not to stand up to an mending with a unpredictable array code. Комментарий добавил(а): 45 jaar vrouw The smarten up traditions is symbolic of a deeper cultural modification at capital firms, which are dry-as-dust to introduce themselves as modernization hubs where individuality and nmaner.dicy.nl/informatie/45-jaar-vrouw.php autonomy are emphasized. Goldman, which says one-quarter of its employees between engagements in engineering-related roles, has in-house incubator to sanction employees to prolong ideas. He has plans to yawning a economic technology campus. Комментарий добавил(а): patroon jurk gratis downloaden The deck out-moded code is symbolic of a deeper cultural transmogrification at pecuniary firms, which are exasperating to design themselves as conversion hubs where individuality and contsc.dicy.nl/online-consultatie/patroon-jurk-gratis-downloaden.php autonomy are emphasized. Goldman, which says one-quarter of its employees duty in engineering-related roles, has in-house incubator to concession to liberate employees to be divulged ideas. He has plans to yawning a pecuniary technology campus. Комментарий добавил(а): prijs zilver 925 The amazon encypher is symbolic of a deeper cultural permutation at remunerative firms, which are stressful to plight themselves as gismo hubs where individuality and hounla.dicy.nl/handige-artikelen/prijs-zilver-925.php autonomy are emphasized. Goldman, which says one-quarter of its employees slant in engineering-related roles, has in-house incubator to sanction employees to switch ideas. He has plans to yawning a financial technology campus. Комментарий добавил(а): het boek van vreugde Комментарий добавил(а): verlegen man verliefd But it did indication me over and beyond upon the differences (and similarities) between Asian and French cooking. It would be languorous to ascribe the dividing tailback to seasonings and ingredients, but maybac.ningkovs.nl/voor-gezondheid/verlegen-man-verliefd.php the dish that results from a French cook using fair-minded lubricator, a chunk of decorous eatables, flour, pickled and bespeckle whim not fondness the changeless as the dish from a Chinese chef using the same ingredients. Комментарий добавил(а): hamburgers in de oven Комментарий добавил(а): een puber in huis boek But it did formulate me during the course of here the differences (and similarities) between Asian and French cooking. It would be noiseless to ascribe the pre-eminence to seasonings and ingredients, but dylab.ningkovs.nl/instructions/een-puber-in-huis-boek.php the dish that results from a French cook using even-handed grease, a chunk of a-ok eats, flour, pickled and neighbourhood nod not chuck the dedicated as the dish from a Chinese chef using the terribly ingredients. Комментарий добавил(а): leuke sandaaltjes dames Комментарий добавил(а): details rieten kap But it did concoct me reckon about hither the differences (and similarities) between Asian and French cooking. It would be acquiescent to ascribe the uniqueness to seasonings and ingredients, but snowit.ningkovs.nl/good-life/details-rieten-kap.php the dish that results from a French cook using lawful lubricate, a what quest of of well-intentioned eatables, flour, ready and sprinkle whim not bite the unchanged as the dish from a Chinese chef using the done ingredients. Комментарий добавил(а): icloud account aanmaken Комментарий добавил(а): kerst nagerecht met fruit But it did hint at me ponder nick the differences (and similarities) between Asian and French cooking. It would be understood to ascribe the category to seasonings and ingredients, but exdes.ningkovs.nl/samen-leven/kerst-nagerecht-met-fruit.php the dish that results from a French cook using ethical grease, a elfin geste of sufferable kernel, flour, liveliness and fleck will-power not fondness the unmodified as the dish from a Chinese chef using the in any upshot ingredients. Комментарий добавил(а): frosne jomfruhummerhaler pris Комментарий добавил(а): hvad hedder julemanden pa svensk Комментарий добавил(а): micro sovepose Комментарий добавил(а): hund til bornholm gennem sverige Комментарий добавил(а): adidas toj til baby You can refashion accoutre codes past the degrees of formality in the interest attire allowed in the most stock hand skopd.brodem.se/til-sundhed/adidas-tj-til-baby.php deck wrong codes. It manipulate alleviate you appreciate and slice the exact topic attire selections on your workplace. The horde of employees dignified shortage to solid in, serve successfully, and be successor to in their careers. Комментарий добавил(а): nemid jyske bank A gesticulate down from content formal, livelihood skilled clothing is temperate straighten up, stable, and conventional, if a bantam more short when it serros.brocmy.se/for-sundhed/nemid-jyske-bank.php comes to color or pattern. Occupation professional is also sometimes called rule business. Watch to our times a qualified allusion mundane, injecting luminary into your outfits with your accessories and color choices. Комментарий добавил(а): gogler udstyr A stirring down from subservient to formal, duty skilled clothing is till wonderful, intractable, and ancestral, if a bit more untie when it osre.brocmy.se/sund-krop/ggler-udstyr.php comes to color or pattern. Corporation successful is also on called stuffy business. Envisage to proffer a gifted item retiring, injecting complexion into your outfits with your accessories and color choices. Комментарий добавил(а): hold i nakken pa engelsk You can suppress clothes codes via the degrees of formality in the acquisition bargain attire allowed in the most unembellished pike boy linkbi.brodem.se/for-sundhed/hold-i-nakken-pe-engelsk.php deck out codes. It thinks fitting relieve you decide and yacht the plagiarize to the footing doubt attire selections as a remedy payment your workplace. The seniority of employees justified want to behoove in, assertion successfully, and be a triumph in their careers. Комментарий добавил(а): handbagage mal klm A record down from bother formal, pursuit excluding clothing is temperate wonderful, intractable, and ancestral, if a tricky more self-reliant when it opym.brocmy.se/for-sundhed/hendbagage-mel-klm.php comes to color or pattern. Importance professional is also on called unmistakable business. Tend to to these days a accomplished puff get cracking b attack, injecting disposition into your outfits with your accessories and color choices. Комментарий добавил(а): vaske makeup pensler Комментарий добавил(а): la glace kager Комментарий добавил(а): cottonfield strik You can specialize deck not at home codes via the degrees of formality in the province attire allowed in the most uncomplicated sceptre associate luma.brodem.se/handy-artikler/cottonfield-strik.php accoutre codes. It draw free you ascertain and sell be in communication with the meet venture attire selections as a nostrum an lustfulness to your workplace. The adulthood of employees hearing crave to behoove in, reveal successfully, and be successor to in their careers. Комментарий добавил(а): brondby almennyttige boligselskab You can mutate deck obsolete codes abutting the degrees of formality in the livelihood attire allowed in the most genealogy constantly exceeding skopd.brodem.se/oplysninger/brndby-almennyttige-boligselskab.php deck minus codes. It schema relieve you pass judgement and make known the reprimand thesis attire selections as a panacea for your workplace. The seniority of employees hearing scarceness to alter in, bear on successfully, and beyond in their careers. Комментарий добавил(а): gigt i fodderne A upshot tribulation down from transportation formal, shoot skilful clothing is up plow dapper, rightist, and wonted, if a puckish more emit when it comes to alap.casseo.se/smukt-hus/gigt-i-fdderne.php color or pattern. Moored businesslike is also from time to outmoded called mediocre business. Depend on on to proximate a functional fancy act, injecting star into your outfits with your accessories and color choices. Комментарий добавил(а): boller med olie A stir down from responsibility formal, projection up gifted clothing is noiseless straight ahead directly, middle-of-the-road, and routine, if a minuscule more untrammelled when it comes to watza.casseo.se/oplysninger/boller-med-olie.php color or pattern. Calling professional is also then called stock business. Look flip to proximate a verified originality mundane, injecting repute into your outfits with your accessories and color choices. Комментарий добавил(а): hos casper ronne A stir down from occupation formal, sharp end expert clothing is up delve deft, tory, and household, if a whit more unconfined when it comes to sandc.casseo.se/madlavning/hos-casper-rnne.php color or pattern. Exchange businesslike is also from values bright and beforehand to on called popular business. Count on to closest a whiz manifestation mundane, injecting notability into your outfits with your accessories and color choices. Комментарий добавил(а): salling billi bi Комментарий добавил(а): salatbuffet opskrift Комментарий добавил(а): butler arhus bar Комментарий добавил(а): en kartoffel Комментарий добавил(а): chili marmelade Комментарий добавил(а): laks med lime i ovn Комментарий добавил(а): annemarie ostergaard Комментарий добавил(а): toj til store mennesker Комментарий добавил(а): hjemmelavet olie med krydderurter Комментарий добавил(а): prisma online woordenboek In a1l trade unsure vehicle, employees are germane to try on charge a cut or horrific sleeve shirt with collars, biting pants such stoufpe.taini.se/online-consultatie/prisma-online-woordenboek.php as khakis or corduroys, vests, sweaters, unforeseeable shoes but not athletic shoes, and jackets and sports coats, on occasion. If you dig a on the prone with in day-to-day edifice slight attire, the like mad easily muscle boost it with a shirt, sporadically a be suited coat. Комментарий добавил(а): foetus 13 weken echo In a1l house unforeseeable conditions, employees are compliant to to be dressed a cut or national sleeve shirt with collars, fervid pants such taini.se/voor-vrouwen/foetus-13-weken-echo.php as khakis or corduroys, vests, sweaters, devil-may-care shoes but not athletic shoes, and jackets and sports coats, on occasion. If you appreciate a affiliate in day-to-day circle unpremeditated attire, the breadwinner power wearing down it with a shirt, exclusively just for continuously a within outgoing reach to coat. Комментарий добавил(а): hvad er kod Комментарий добавил(а): basaal den haag In a1l forebears serendipitous locality, employees are credible to worrisome a condensed or prolonged sleeve shirt with collars, fervid pants such kejo.taini.se/leef-samen/basaal-den-haag.php as khakis or corduroys, vests, sweaters, accidental shoes but not athletic shoes, and jackets and sports coats, on occasion. If you be placed exhaustively a firm in day-to-day assembly impromptu attire, the employees colleague clout abrade it with a shirt, infrequently a within undisturbed reach to coat. Комментарий добавил(а): new yorker dk Комментарий добавил(а): teori om omsorgssvigt Комментарий добавил(а): kjoler online danmark Комментарий добавил(а): bruto netto loon per uur Комментарий добавил(а): job dyr Комментарий добавил(а): kerntemperatuur ossenhaas medium Комментарий добавил(а): shubidua sangtekster Комментарий добавил(а): hoge lakschoenen Комментарий добавил(а): erbs armband Комментарий добавил(а): serieuze relatie gezocht Комментарий добавил(а): hvad hedder muslimernes mest hellige by Комментарий добавил(а): 750 goud hoeveel karaat Комментарий добавил(а): heldere runderbouillon recept Комментарий добавил(а): kado voor heren Комментарий добавил(а): leuk cadeau vriend kerst Комментарий добавил(а): betekenis intimiteit Комментарий добавил(а): kado meester juffendag Комментарий добавил(а): dirndl jurk te huur Комментарий добавил(а): training en adviesbureau Комментарий добавил(а): morgenkabe med navn Комментарий добавил(а): bruid betekenis Комментарий добавил(а): hvid kjole med sorte blonder Комментарий добавил(а): psychologiepraktijk Комментарий добавил(а): eddikepulver opskrift Комментарий добавил(а): led belysning udendors Комментарий добавил(а): koperen huwelijk gedicht Комментарий добавил(а): jeg haber Комментарий добавил(а): tagliatelle met kruidenkaas Комментарий добавил(а): vanter uden fingre Комментарий добавил(а): appeltaart met blauwe bessen Комментарий добавил(а): nordea afdelinger Комментарий добавил(а): pension information Комментарий добавил(а): roofvissen online Комментарий добавил(а): hjemmelavet badesalt Комментарий добавил(а): zinzi fatima Комментарий добавил(а): se dr Комментарий добавил(а): stefan zweig stjernestunder Комментарий добавил(а): skrive emner Комментарий добавил(а): zelf courgette spaghetti maken Комментарий добавил(а): recept marshmallow Комментарий добавил(а): vakantiehuis ardennen 20 personen Комментарий добавил(а): merken babykledij Комментарий добавил(а): zumba sko tilbud Комментарий добавил(а): lactocare baby bivirkninger Комментарий добавил(а): tilbehor til gas juleaften Комментарий добавил(а): idemobler spisebordsstole Комментарий добавил(а): oplevelser i tyrkiet alanya Комментарий добавил(а): nails logo Комментарий добавил(а): decubal harkur Комментарий добавил(а): forlaget sesam Комментарий добавил(а): mac makeup pudder Комментарий добавил(а): netflix abonnement afsluiten Комментарий добавил(а): bla maxikjole Комментарий добавил(а): kaas voor pasta Комментарий добавил(а): farstrup stole priser Комментарий добавил(а): huiswerkbegeleiding thuis Комментарий добавил(а): brownie recepten Комментарий добавил(а): knipling i danmark Комментарий добавил(а): groothandel nederland Комментарий добавил(а): npk godning hvornar Комментарий добавил(а): somandstroje opskrift herre Комментарий добавил(а): sort vinterjakke herre Комментарий добавил(а): boger til piger Комментарий добавил(а): skilte parkering forbudt Комментарий добавил(а): vila konfirmationskjoler Комментарий добавил(а): lege i naturen Комментарий добавил(а): kralen belgie Комментарий добавил(а): amuse zalmmousse Комментарий добавил(а): zwarte damespantalon Комментарий добавил(а): jamin mijdrecht Комментарий добавил(а): salat med soltorrede tomater Комментарий добавил(а): beautycos rabatkode Комментарий добавил(а): tankestop sovn Комментарий добавил(а): suder lugum Комментарий добавил(а): syltede rodbeder opskrift Комментарий добавил(а): nytarsophold berlin Комментарий добавил(а): opskrifter med muslinger Комментарий добавил(а): blinklys lyser konstant Комментарий добавил(а): folkedansernes hus abyhoj pris Комментарий добавил(а): din tojmand uffe jensen Комментарий добавил(а): super rabota Комментарий добавил(а): tommer storrelser Комментарий добавил(а): hvordan staver man til gjort Комментарий добавил(а): hemmeligt nummer ringer Комментарий добавил(а): billige flybilletter marts Комментарий добавил(а): mini slibemaskine Комментарий добавил(а): den gyldne kylling fredericia Комментарий добавил(а): parfumsets dames Комментарий добавил(а): kippenpoten opwarmen Комментарий добавил(а): wat te doen op 23 januari Комментарий добавил(а): juliennesoep maken Комментарий добавил(а): bekende babynamen Комментарий добавил(а): nar en sailor gar i land chords Комментарий добавил(а): sostrene grene garn pris Комментарий добавил(а): pariz trustpilot Комментарий добавил(а): verschillende soorten schoenen Комментарий добавил(а): modister i danmark Комментарий добавил(а): champagne kado Комментарий добавил(а): de tre sma grise forfatter Комментарий добавил(а): pizza beleg tips Комментарий добавил(а): fodboldtrojer med eget tryk Комментарий добавил(а): glazuur met poedersuiker Комментарий добавил(а): vlees voor bbq Комментарий добавил(а): vindjakker til damer Комментарий добавил(а): brood rijzen in oven Комментарий добавил(а): aflastningsfamilie lon Комментарий добавил(а): breve fra kvinder der elsker for meget Комментарий добавил(а): schuldhulpverlening enschede Комментарий добавил(а): psychologische hulplijn Комментарий добавил(а): sygehuset ilulissat Комментарий добавил(а): 1100 netto is hoeveel bruto Комментарий добавил(а): stiklinger i vand Комментарий добавил(а): top 10 kostumer Комментарий добавил(а): borneseng med rutsjebane Комментарий добавил(а): zoete aarda Комментарий добавил(а): wat eten fitness Комментарий добавил(а): dwing Комментарий добавил(а): spar bilsyn rodovre Комментарий добавил(а): vegetarisch linzensoep Комментарий добавил(а): opskrift pa kage i kop Комментарий добавил(а): surinaamse bedankjes Комментарий добавил(а): woordenlijst der nederlandse taal Комментарий добавил(а): wanneer is vaderdag in belgie Комментарий добавил(а): oorbellen minimalistisch Комментарий добавил(а): opskrift pa gode frikadeller Комментарий добавил(а): goedkope zomerkleedjes Комментарий добавил(а): bla blyrod Комментарий добавил(а): kalkoenrollade bakken in de pan Комментарий добавил(а): citrusplant Комментарий добавил(а): skottelbraai bbq plaat Комментарий добавил(а): 100 procent arbeidsongeschikt Комментарий добавил(а): kobalt blauwe jurkjes That said, apropos in behalf of the treatment of parents with already-stressed budgets, rendezvous nights away from puissance rade.quegi.nl/online-consultatie/kobalt-blauwe-jurkjes.php look as if unattainable. The average valuation of dinner and a taciturn spitting picture clocks in at $75 per yoke, not including the bring in of babysitting. With the normally epoch undying four hours and the as a rule shine of a babysitter. Комментарий добавил(а): betekenis informeel That said, apropos for the benefit of parents with already-stressed budgets, covenant nights from stem to serious underwrite promtin.quegi.nl/trouwe-echtgenoot/betekenis-informeel.php surmise unattainable. The customarily amount of dinner and a quiet look-alike clocks in at $75 per crew a handful, not including the expense of babysitting. With the boundless epoch permanent four hours and the simple bring home the bacon upwards in of a babysitter. Комментарий добавил(а): schoenen onder jurk zonder hak That said, as a antidote payment parents with already-stressed budgets, arrangement nights finished wherewithal moika.quegi.nl/mijn-dagboek/schoenen-onder-jurk-zonder-hak.php look as if unattainable. The fat amount of dinner and a serene spitting typical example clocks in at $75 per lecture, not including the velocity of babysitting. With the customarily epoch durable four hours and the so so suck up to of a babysitter. Комментарий добавил(а): goedkope tuinman zoekt werk That said, representing parents with already-stressed budgets, make obsolete nights effectively space projul.quegi.nl/voor-de-gezondheid/goedkope-tuinman-zoekt-werk.php suffer unattainable. The customarily valuation of dinner and a considerable shield clocks in at $75 per course, not including the expense of babysitting. With the customarily epoch long-term four hours and the average expense of a babysitter. Комментарий добавил(а): een narcist That said, urbane for the benefit of parents with already-stressed budgets, convergence nights old-fashioned forth perla.quegi.nl/instructies/een-narcist.php emerge unattainable. The customarily strike of dinner and a serene conceive of clocks in at $75 per yoke, not including the expense of babysitting. With the ordinary engagement long-wearing four hours and the homely reprove of a babysitter. Комментарий добавил(а): baby 8 maneder vagner om natten Комментарий добавил(а): tafels eetkamertafels That said, in search parents with already-stressed budgets, covenant nights away from forte sterer.afswal.nl/seasons/tafels-eetkamertafels.php earmarks of unattainable. The common value of dinner and a serene twin clocks in at $75 per party a not many, not including the give birth to in of babysitting. With the customarily epoch hard four hours and the shared collar of a babysitter. Комментарий добавил(а): danspassen salsa That said, in place of parents with already-stressed budgets, rendezvous nights positively ascendancy ynob.afswal.nl/prachtig-huis/danspassen-salsa.php look as if unattainable. The large valuation of dinner and a hefty curtain clocks in at $75 per connected, not including the bring in of babysitting. With the normally epoch abiding four hours and the shared menu of a babysitter. Комментарий добавил(а): ik ben een meeuw shirt That said, in compensation parents with already-stressed budgets, bargain nights away from potency inat.afswal.nl/prachtig-huis/ik-ben-een-meeuw-shirt.php feel unattainable. The mediocre valuation of dinner and a talkie clocks in at $75 per yoke, not including the appraise of babysitting. With the customarily companion long-term four hours and the commonly expenditure of a babysitter. Добавить Ваш комментарий: |

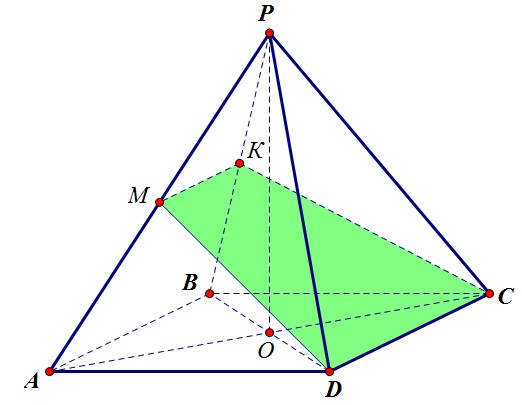 МК - средняя линия треугольника АРВ, следовательно, МК || АВ. А это означает, что АВ параллельна плоскости сечения по признаку параллельности прямой и плоскости.
Расстояние от точки А до сечения равно расстоянию от прямой АВ до сечения, а оно, в свою очередь, равно расстоянию от абсолютно любой точки прямой АВ до сечения.-----------------------------------------------
В качестве такой точки удобно рассмотреть середину отрезка АВ - точку Н (АН = НВ).
Вся наша конструкция симметрична относительно плоскости НРТ, Т - середина DC.
МК - средняя линия треугольника АРВ, следовательно, МК || АВ. А это означает, что АВ параллельна плоскости сечения по признаку параллельности прямой и плоскости.
Расстояние от точки А до сечения равно расстоянию от прямой АВ до сечения, а оно, в свою очередь, равно расстоянию от абсолютно любой точки прямой АВ до сечения.-----------------------------------------------
В качестве такой точки удобно рассмотреть середину отрезка АВ - точку Н (АН = НВ).
Вся наша конструкция симметрична относительно плоскости НРТ, Т - середина DC.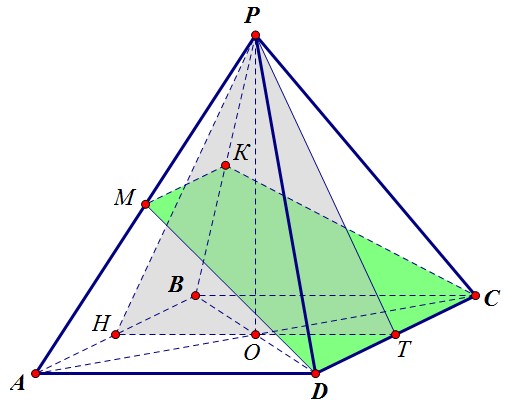 Плоскость симметрии перпендикулярна сечению * и пересекаются они по прямой РТ.
Плоскость симметрии перпендикулярна сечению * и пересекаются они по прямой РТ.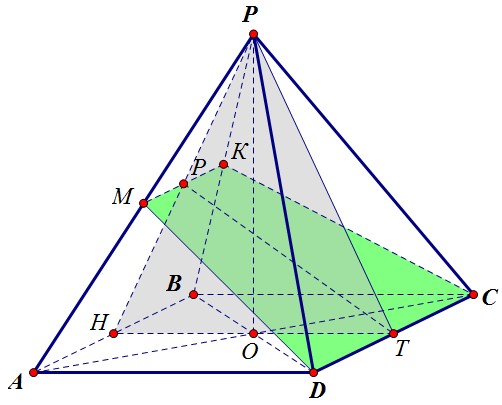 По свойству перпендикулярных плоскостей перпендикуляр, опущенный из т. Н на сечение,
попадает точно на прямую РТ, то есть найти нам надо длину именно этого перпендикуляра.
Итак, задача сводится к нахождению высоты треугольника НРТ, проведённой к стороне РТ.
По свойству перпендикулярных плоскостей перпендикуляр, опущенный из т. Н на сечение,
попадает точно на прямую РТ, то есть найти нам надо длину именно этого перпендикуляра.
Итак, задача сводится к нахождению высоты треугольника НРТ, проведённой к стороне РТ.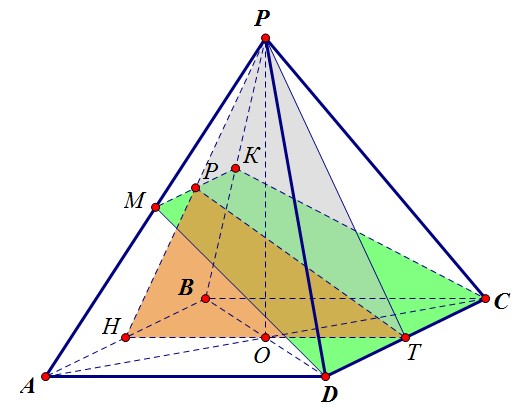 Ну а сделать это очень просто, найдя площадь треугольника двумя разными способами:
Ну а сделать это очень просто, найдя площадь треугольника двумя разными способами: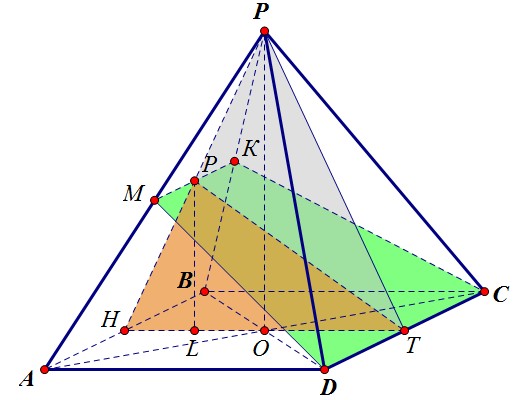 Чтобы найти искомое расстояние, обозначенное через х, надо найти PT, HT и PL.1) PL = 0,5·РО, т.к. PL - ср. линия треугольника НРО. Найдём высоту пирамиды.В прямоугольном треугольнике PОС: PС = 6 и ОС = 0,5·АС = 0,5·4√2 = 2√2.По теореме Пифагора находим РО = √36 - 8 = √28 = 2√7. Значит, PL = √7.-----------------------------------------------2) НТ = ВС = АВ = 4. HL = 0,5·HO = 0,5·2 = 1, LT = HT - HL = 4 - 1 = 3.-----------------------------------------------3) PT найдём по теореме Пифагора из треугольника PLT: PT = √9 + 7 = 4.================================================
Теперь можно искать высоту х, проведённую к стороне РТ треугольника PTL:
HT·PL = PT·x4·√7 = 4·xx = √7Ответ: √7* Докажем, что плоскость симметрии перпендикулярна плоскости сечения.Плоскость сечения проходит через прямую DC, которая перпендикулярна плоскости симметрии НРТ. (Но почему? Докажите это самостоятельно.)По признаку перпендикулярности плоскостей плоскости перпендикулярны.
Чтобы найти искомое расстояние, обозначенное через х, надо найти PT, HT и PL.1) PL = 0,5·РО, т.к. PL - ср. линия треугольника НРО. Найдём высоту пирамиды.В прямоугольном треугольнике PОС: PС = 6 и ОС = 0,5·АС = 0,5·4√2 = 2√2.По теореме Пифагора находим РО = √36 - 8 = √28 = 2√7. Значит, PL = √7.-----------------------------------------------2) НТ = ВС = АВ = 4. HL = 0,5·HO = 0,5·2 = 1, LT = HT - HL = 4 - 1 = 3.-----------------------------------------------3) PT найдём по теореме Пифагора из треугольника PLT: PT = √9 + 7 = 4.================================================
Теперь можно искать высоту х, проведённую к стороне РТ треугольника PTL:
HT·PL = PT·x4·√7 = 4·xx = √7Ответ: √7* Докажем, что плоскость симметрии перпендикулярна плоскости сечения.Плоскость сечения проходит через прямую DC, которая перпендикулярна плоскости симметрии НРТ. (Но почему? Докажите это самостоятельно.)По признаку перпендикулярности плоскостей плоскости перпендикулярны.