|
В окружность радиуса R вписан треугольник АВС. Вторая окружность радиуса r,
концентрическая с первой, касается одной стороны треугольника и делит каждую из двух других сторон на три равные части.
а) Докажите, что треугольник АВС равнобедренный.
б) Найдите r:R.
Доказательство. Способ 1.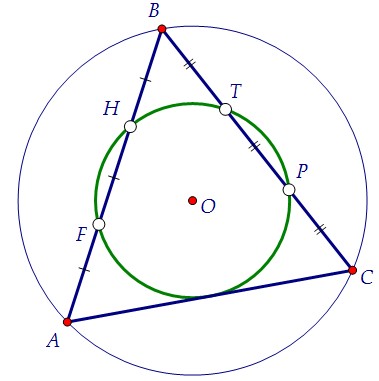 Идея доказательства состоит в том, что четырёхугольник FHTP вписан в окружность.
Если четырёхугольник окажется трапецией, то обязательно равнобедренной.
Идея доказательства состоит в том, что четырёхугольник FHTP вписан в окружность.
Если четырёхугольник окажется трапецией, то обязательно равнобедренной.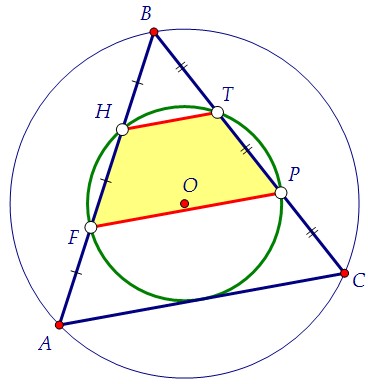 HT || FP по очень простой причине: HT - средняя линия треугольника FBP. HT || FP по очень простой причине: HT - средняя линия треугольника FBP.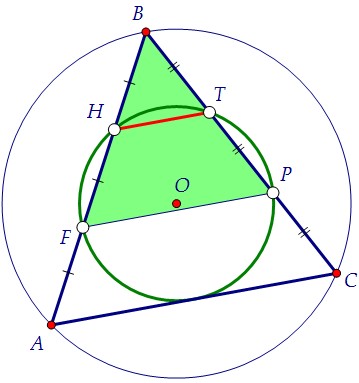 Вписанная в окружность трапеция является равнобедренной, FH = PT.FH и PT составляют трети сторон АВ и СВ. Следовательно, АВ = СВ.
Доказательство. Способ 2. Вписанная в окружность трапеция является равнобедренной, FH = PT.FH и PT составляют трети сторон АВ и СВ. Следовательно, АВ = СВ.
Доказательство. Способ 2.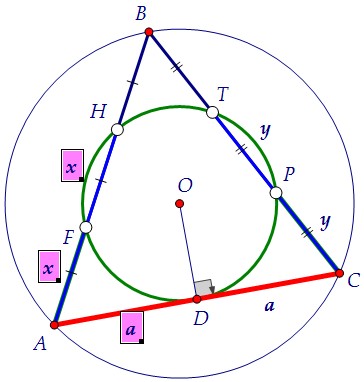 Т.к. точка О является центром описанной около треугольника АВС окружности,то она лежит на серединном перпендикуляре к АС, D - середина АС, ОD ⊥ АС. Вторая окружность с тем же центром О касается АС в точке D, ОD - её радиус.
По свойству секущих и касательных, проведённых из одной точки А, имеем:AD2 = AF · AH или а2 = х · (2х) = 2х2, где х = AF, a = AD.
По свойству секущих и касательных, проведённых из одной точки C, имеем:CD2 = CP · CT или а2 = y · (2y) = 2y2, где y = CP, a = CD.
Отсюда x = y, а значит, АВ = АС. Кроме того, мы получили, что а = х√2.====================================
В равнобедренном треугольнике АВС точка О лежит на высоте (медиане) АD. В прямоугольном треугольнике АВD стороны АD = х√2, АВ = 3х, ВD = х√7.
Т.к. точка О является центром описанной около треугольника АВС окружности,то она лежит на серединном перпендикуляре к АС, D - середина АС, ОD ⊥ АС. Вторая окружность с тем же центром О касается АС в точке D, ОD - её радиус.
По свойству секущих и касательных, проведённых из одной точки А, имеем:AD2 = AF · AH или а2 = х · (2х) = 2х2, где х = AF, a = AD.
По свойству секущих и касательных, проведённых из одной точки C, имеем:CD2 = CP · CT или а2 = y · (2y) = 2y2, где y = CP, a = CD.
Отсюда x = y, а значит, АВ = АС. Кроме того, мы получили, что а = х√2.====================================
В равнобедренном треугольнике АВС точка О лежит на высоте (медиане) АD. В прямоугольном треугольнике АВD стороны АD = х√2, АВ = 3х, ВD = х√7.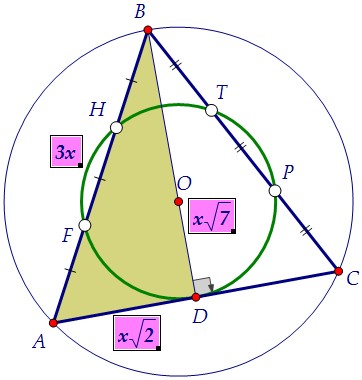 Заметьте! В треугольнике АВD мы сможем найти любой острый угол.
От нас требуется найти r:R, а это то же самое, что косинус угла AOD. Заметьте! В треугольнике АВD мы сможем найти любой острый угол.
От нас требуется найти r:R, а это то же самое, что косинус угла AOD.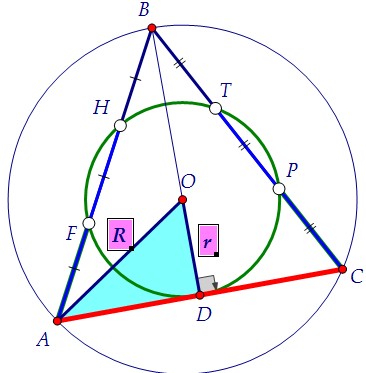 Угол AOD - центральный и равен величине дуги, на которую опирается. Угол AOD - центральный и равен величине дуги, на которую опирается.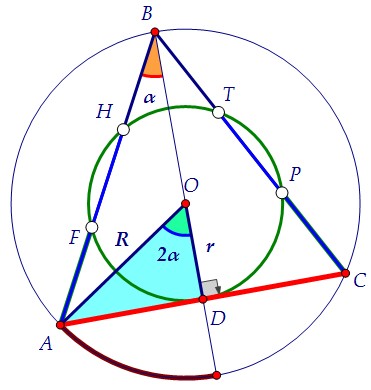 Угол AВD - вписанный, и он в два раза меньше той же самой дуги.Пусть ∠AВD = α, тогда ∠AОD = 2α. Найдём cos2α = cos2α - sin2α.Вернёмся к треугольнику АВD (см. выше), чтобы найти sinα и cosα. Угол AВD - вписанный, и он в два раза меньше той же самой дуги.Пусть ∠AВD = α, тогда ∠AОD = 2α. Найдём cos2α = cos2α - sin2α.Вернёмся к треугольнику АВD (см. выше), чтобы найти sinα и cosα.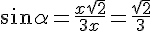 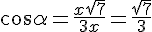 И наконец, ищем косинус двойного угла (а значит, нужное отношение): И наконец, ищем косинус двойного угла (а значит, нужное отношение):
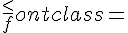 {R}=cos{(2\alpha)}=cos^2{\alpha}-sin^2{\alpha}=\frac{7}{9}-\frac{2}{9}=\frac{5}{9}'>Ответ: 5:9 {R}=cos{(2\alpha)}=cos^2{\alpha}-sin^2{\alpha}=\frac{7}{9}-\frac{2}{9}=\frac{5}{9}'>Ответ: 5:9 Автор: Ольга Себедаш Просмотров: 11284
|

 Идея доказательства состоит в том, что четырёхугольник FHTP вписан в окружность.
Если четырёхугольник окажется трапецией, то обязательно равнобедренной.
Идея доказательства состоит в том, что четырёхугольник FHTP вписан в окружность.
Если четырёхугольник окажется трапецией, то обязательно равнобедренной. HT || FP по очень простой причине: HT - средняя линия треугольника FBP.
HT || FP по очень простой причине: HT - средняя линия треугольника FBP. Вписанная в окружность трапеция является равнобедренной, FH = PT.FH и PT составляют трети сторон АВ и СВ. Следовательно, АВ = СВ.
Доказательство. Способ 2.
Вписанная в окружность трапеция является равнобедренной, FH = PT.FH и PT составляют трети сторон АВ и СВ. Следовательно, АВ = СВ.
Доказательство. Способ 2. Т.к. точка О является центром описанной около треугольника АВС окружности,то она лежит на серединном перпендикуляре к АС, D - середина АС, ОD ⊥ АС. Вторая окружность с тем же центром О касается АС в точке D, ОD - её радиус.
По свойству секущих и касательных, проведённых из одной точки А, имеем:AD2 = AF · AH или а2 = х · (2х) = 2х2, где х = AF, a = AD.
По свойству секущих и касательных, проведённых из одной точки C, имеем:CD2 = CP · CT или а2 = y · (2y) = 2y2, где y = CP, a = CD.
Отсюда x = y, а значит, АВ = АС. Кроме того, мы получили, что а = х√2.====================================
В равнобедренном треугольнике АВС точка О лежит на высоте (медиане) АD. В прямоугольном треугольнике АВD стороны АD = х√2, АВ = 3х, ВD = х√7.
Т.к. точка О является центром описанной около треугольника АВС окружности,то она лежит на серединном перпендикуляре к АС, D - середина АС, ОD ⊥ АС. Вторая окружность с тем же центром О касается АС в точке D, ОD - её радиус.
По свойству секущих и касательных, проведённых из одной точки А, имеем:AD2 = AF · AH или а2 = х · (2х) = 2х2, где х = AF, a = AD.
По свойству секущих и касательных, проведённых из одной точки C, имеем:CD2 = CP · CT или а2 = y · (2y) = 2y2, где y = CP, a = CD.
Отсюда x = y, а значит, АВ = АС. Кроме того, мы получили, что а = х√2.====================================
В равнобедренном треугольнике АВС точка О лежит на высоте (медиане) АD. В прямоугольном треугольнике АВD стороны АD = х√2, АВ = 3х, ВD = х√7. Заметьте! В треугольнике АВD мы сможем найти любой острый угол.
От нас требуется найти r:R, а это то же самое, что косинус угла AOD.
Заметьте! В треугольнике АВD мы сможем найти любой острый угол.
От нас требуется найти r:R, а это то же самое, что косинус угла AOD. Угол AOD - центральный и равен величине дуги, на которую опирается.
Угол AOD - центральный и равен величине дуги, на которую опирается. Угол AВD - вписанный, и он в два раза меньше той же самой дуги.Пусть ∠AВD = α, тогда ∠AОD = 2α. Найдём cos2α = cos2α - sin2α.Вернёмся к треугольнику АВD (см. выше), чтобы найти sinα и cosα.
Угол AВD - вписанный, и он в два раза меньше той же самой дуги.Пусть ∠AВD = α, тогда ∠AОD = 2α. Найдём cos2α = cos2α - sin2α.Вернёмся к треугольнику АВD (см. выше), чтобы найти sinα и cosα.