Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найти все значения параметра, при каждом из которых уравнение



имеет по крайней мере два корня, один из которых неотрицателен,
а другой не превосходит -1.

Уравнение выглядит довольно страшно. Сделаем некоторые замены.
((2x + a)·b - 2(x² + x))·c = 0
Преобразуем немного выражение в скобках, которое зависит от х.
с·(2bx + ab - 2x² - 2x) = 0
Не правда ли, в таком виде уравнение смотрится намного проще?
с·(2x² - 2(b - 1)x - ab) = 0
Идея решения.
1) Если с = 0 (и при этом сохраняет смысл сложный параметр b),
то переменная х может принимать любые действительные значения,
в том числе и те, о которых говорится в условии. Нас это устраивает.
2) Если с ≠ 0 и все параметры имеют смысл, то квадратный трёхчлен
должен иметь два корня х₁ и х₂, при этом х₁ ≤ -1 и х₂ ≥ 0.
=============================================
Найдём, при каких значениях а имеют смысл параметры b и с:
22а - 4а² - 24 ≥ 0                 36а - 9а² > 0
2а² - 11а + 12 ≤ 0                а² - 4а < 0
1,5 ≤ а ≤ 4                          0 < а < 4  
Вывод: 1,5 ≤ а < 4.
=============================================
Итак, рассмотрим первый случай и приравняем коэффициент с нулю.









           
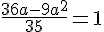
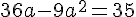
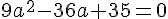
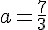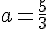Убедиться, что не теряет смысл параметр b, можно как угодно.
=============================================
Рассмотрим теперь второй случай и потребуем, чтобы х₁ ≤ -1 и х₂ ≥ 0.
Это означает, что отрезок [-1; 0] должен находиться между корнями.
А это значит, что функция f(x) = 2x² - 2(b - 1)x - ab на отрезке [-1; 0]
должна быть неположительной. Для этого потребуем одновременное
выполнение двух неравенств: f(-1) ≤ 0 и f(0) ≤ 0.
-----------------------------------------------
f(-1) = 2 + 2(b - 1) - ab = 2b - ab = b(2 - a) ≤ 0
f(0) = -ab ≤ 0;                              ab ≥ 0
-----------------------------------------------
Так как 1,5 ≤ а < 4, то рассматриваемые значения а положительны.
Параметр b = √22а - 4а² - 24 неотрицателен на области определения.
Возможны варианты (при условии сохранения смысла параметров):
а) b = 0                б) а ≥ 2
b = 0 при а = 1,5 и а = 4, но при а = 4 теряет смысл логарифм.
Условие а ≥ 2 пересечём с условием 1,5 ≤ а < 4, получим: 2 ≤ а < 4.
Заметим, что число 7/3 в данный промежуток входит.

Ответ: 1,5; 5/3; [2; 4)

Автор: Ольга Себедаш             Просмотров: 6566