Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В кубе ABCDA₁B₁C₁D₁ плоскость проходит через прямую A₁B₁ и середину ребра DD₁.
Найти расстояние от середины ребра CD до плоскости, если ребро куба равно 4.

Построить плоскость сечения просто. Достаточно через точку Т - середину ребра DD₁
провести в плоскости DD₁C₁C прямую ТК параллельно A₁B₁ (точка К - середина СС₁).
Сечение обязательно пересечёт параллельные грани по параллельным прямым.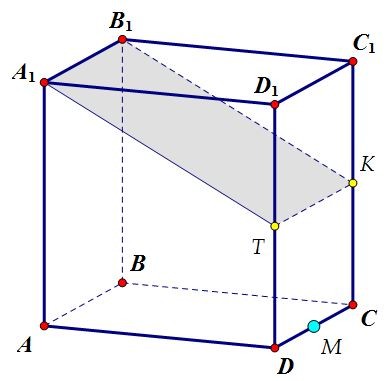



CD параллельна плоскости сечения по признаку параллельности прямой и плоскости.
Расстояния от всех точек прямой CD (в том числе и от точки М - середины отрезка CD)
до плоскости сечения одинаковы. Удобнее искать расстояние до сечения от точки D.



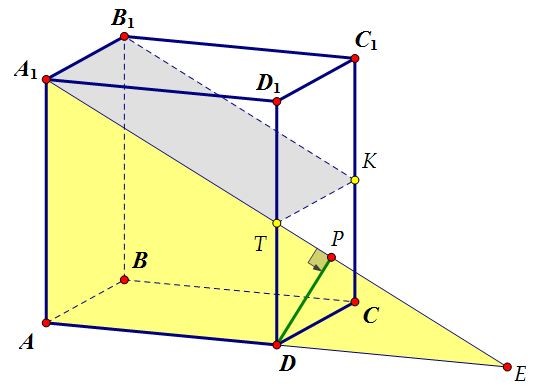Т.к. точка D лежит в плоскости AA₁D₁D, перпендикулярной сечению, значит, расстояние
от точки D до плоскости сечения - это расстояние от точки D до прямой А₁Т, по которой
пересекаются перпендикулярные плоскости, т.е. отрезок DP, перпендикулярный А₁Е.
(докажите, что DP ⊥ А₁В₁КТ по признаку перпендикулярности прямой и плоскости).

Длину DP можно искать из подобия треугольников DPЕ и А₁АЕ. Но можно ещё проще: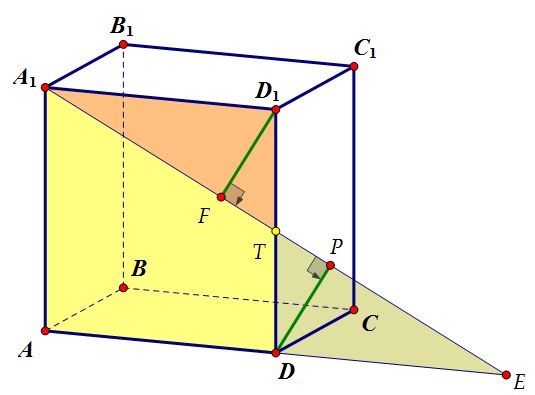



Треугольники DТЕ и D₁ТА₁ равны. Значит, равны и их соответствующие высоты.
Будем искать высоту D₁F треугольника D₁ТА₁, опущенную на гипотенузу А₁Т.



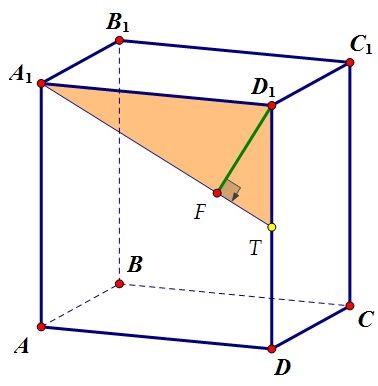D₁А₁ = 4,           D₁Т = 2,           А₁Т = √4² + 2² = √20 = 2√5
Площадь прямоугольного треугольника можно искать двумя разными способами.
S_D1ТА1 = 0,5 · D₁А₁ · D₁Т = 0,5 · А₁T · D₁F
S_D1ТА1 = 0,5 · 4 · 2 = 0,5 · 2√5 · D₁F



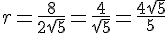Можно искать высоту и в жёлтом треугольнике АА₁Е, а затем разделить её на два.

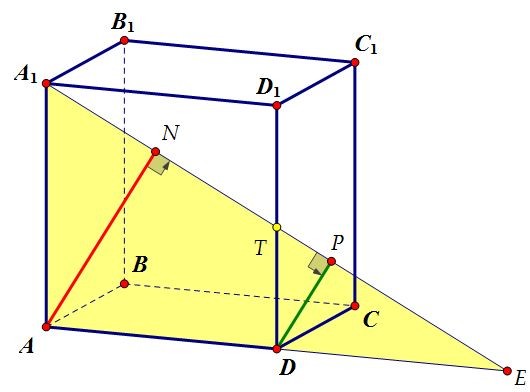Автор: Ольга Себедаш             Просмотров: 14909