Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В треугольнике АВС точка О - центр описанной окружности, точка R лежит на отрезке ВС
и BR = RC. Описанная около треугольника BRO окружность пересекает АВ в точке Т.
Известно, что угол BOR равен 30 градусов, RT = 8, BT = 6.
а) Докажите, что  TR || AC.
б) Найдите площадь треугольника АВС.

Прежде всего опишем окружность вокруг треугольника АВС. При этом заметим,
что центром окружности О является точка пересечения серединных
перпендикуляров, проведённых к сторонам треугольника.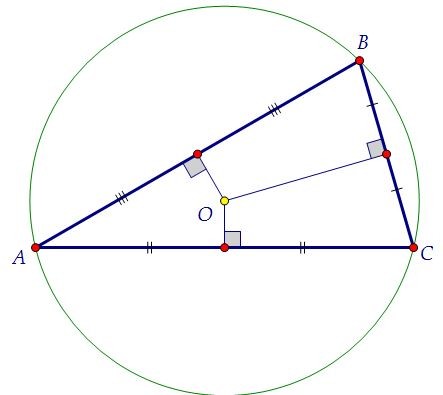



Точка R, о которой идёт речь в условие, является основанием одного из них.



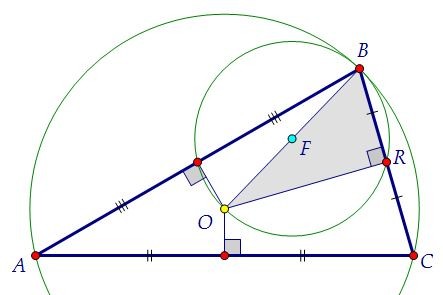Треугольник BRO, таким образом, является прямоугольным. Центр F окружности,
описанной около треугольника BRO, лежит на середине его гипотенузы OB.
Вписанный угол OТB является прямым. Но перпендикуляр, проведённый
из точки O на АB, - серединный перпендикуляр. Значит, Т - середина АВ.



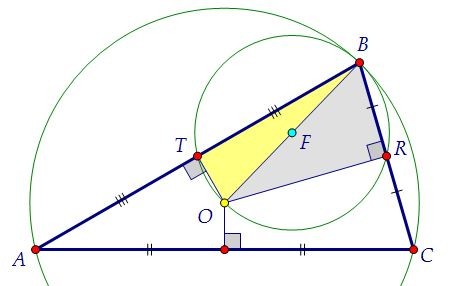Отрезок, соединяющий середины сторон треугольника, является его средней линией.
По свойству средней линии она параллельна третьей стороне, т.е. TR || AC, ч.т.д.

Угол BOR, равный по условию 30°, является половиной центрального угла BOС.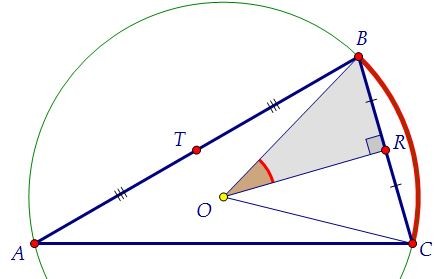



Вписанный угол BАС опирается на ту же дугу, что и центральный угол BOС,
и равен половине дуги, на которую опирается. Значит, ∠BАС = ∠ВOR = 30°.



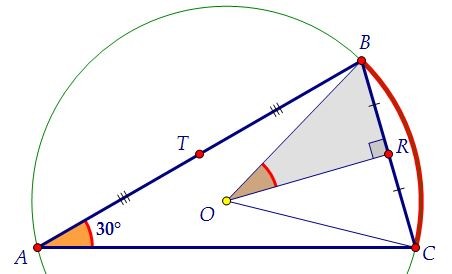Найдём стороны треугольника АВС: АВ = 2·ВТ = 12, АС = 2·TR = 16.



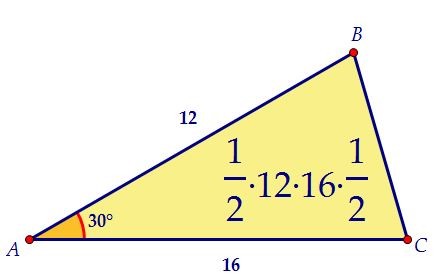Найдём теперь площадь треугольника АВС: S = 0,5·AB·AC·sin30° = 48.

Ответ: 48

Автор: Ольга Себедаш             Просмотров: 12152