Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M.
Точки A₂, B₂ и C₂ — середины отрезков MA, MB и MC соответственно.
а) Докажите, что площадь шестиугольника A₁B₂C₁A₂B₁C₂ вдвое меньше площади треугольника ABC.
б) Найдите сумму квадратов всех сторон этого шестиугольника, если известно, что AB = 5, BC = 8 и AC = 10.

Чертёж к задаче сделать нетрудно. Изобразим медианы и середины нужных отрезков.



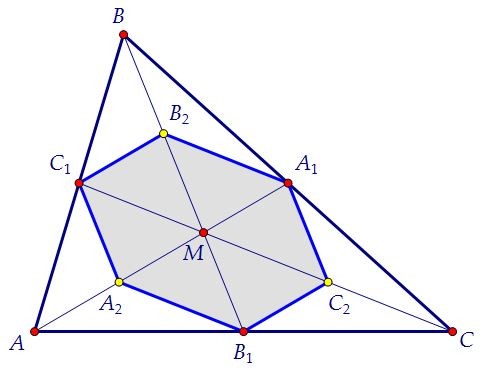Но прежде чем рисовать шестиугольник, обратим внимание сразу на треугольник А₂В₂С₂.



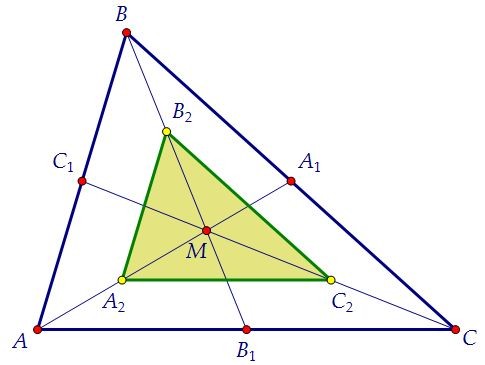Его площадь равна четверти от площади треугольника АВС. Докажем этот очевидный факт.
А₂С₂ средняя линия треугольника АМС. Треугольники АМС и А₂МС₂ подобны с k = 2.



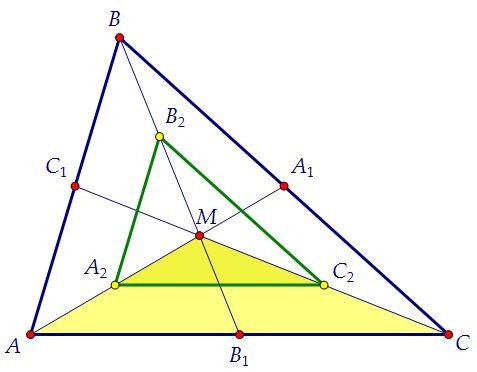Значит, площадь треугольника А₂МС₂ в 4 раза меньше площади треугольника АМС.
Аналогично рассматриваем треугольники А₂МВ₂ и В₂МС₂. Итак, S_ABC = 4·S_А2В2С2.



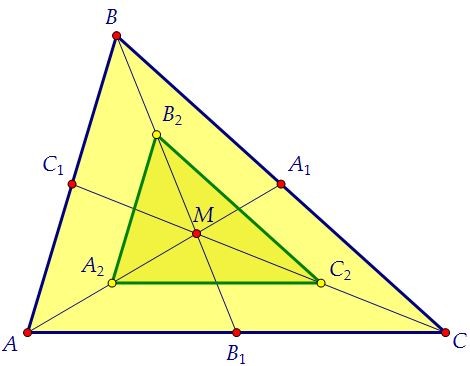Треугольник А₂В₂С₂ составляет только часть шестиугольника A₁B₂C₁A₂B₁C₂.
Рассмотрим теперь треугольник А₂В₁С₂ - один из трёх отрезанных "уголков".



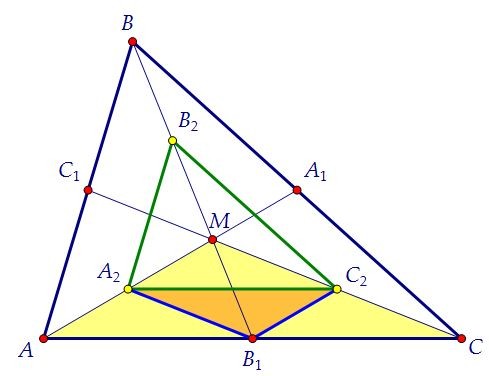Его площадь составляет также одну четверть от площади треугольника АМС.
Для этого заметим, что треугольники А₂В₁С₂ и А₂МС₂ равны по трём сторонам.
Вместе площади А₂В₁С₂, А₂С₁В₂ и В₂А₁С₂ составляют 0,25 от площади АВС.



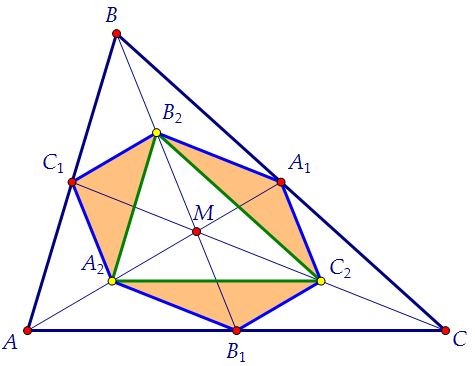Сумма площадей А₂В₂С₂, А₂В₁С₂, А₂С₁В₂ и В₂А₁С₂ составляет 0,5 от площади АВС.



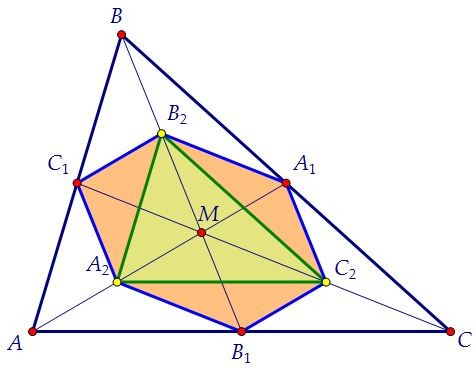Пусть в треугольнике АВС а = ВС, b = AC, c = АC, стороны шестиугольника x, y, z.
Для поиска суммы квадратов сторон шестиугольника воспользуемся утверждением:
Сумма квадратов сторон параллелограмма равна сумме квадратов его диагоналей.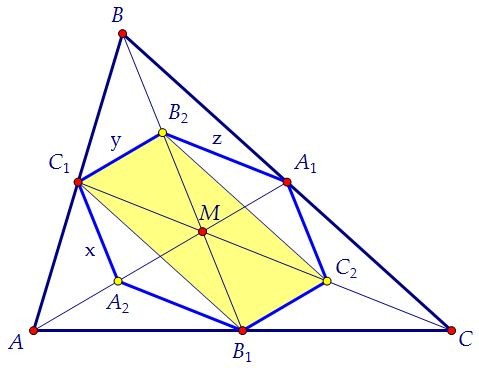



С₁В₂ - средняя линия треугольника АВМ, В₁С₂ - средняя линия треугольника АСМ.
Следовательно, С₁В₂ = В₁С₂ и С₁В₂ || В₁С₂, и поэтому С₁В₂С₂В₁ - параллелограмм.
Кроме того, учитывая свойства медиан, получаем, что А₂М = С₁В₂ = В₁С₂ = y.
Аналогично, В₂М = х и С₂М = z. Кроме того, В₁С₁ = В₂С₂ = 0,5а. Наконец, имеем:
y² + y² + 0,25a² + 0,25a² = 4x² + 4z²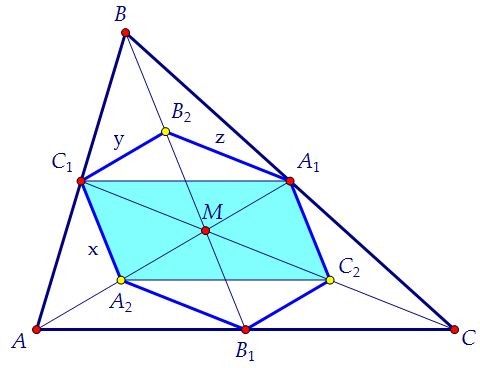



Четырёхугольник А₂С₁А₁С₂ - тоже параллелограмм. И в нём имеем аналогично:
х² + х² + 0,25b² + 0,25b² = 4y² + 4z²



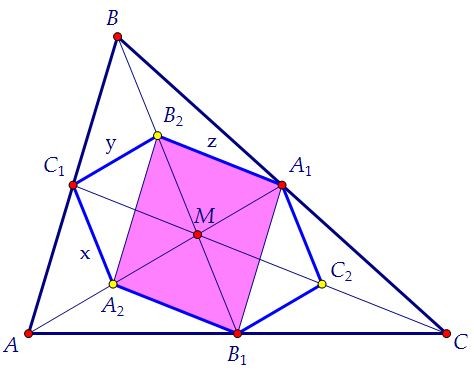Четырёхугольник B₂A₁B₁A₂ - тоже параллелограмм. И в нём имеем аналогично:
z² + z² + 0,25c² + 0,25c² = 4x² + 4y²

Складывая получившиеся три равенства и преобразовывая уравнение, получим:

2х² + 2y² + 2z² = 8х² + 8y² + 8z² - 0,5a² - 0,5b² - 0,5c²

6х² + 6y² + 6z² = 0,5(a² + b² + c²)



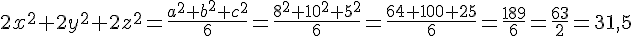Ответ: 31,5

Автор: Ольга Себедаш             Просмотров: 29673