Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

На основании ВС трапеции ABCD взята точка Е, лежащая на одной окружности
с точками А, С и D. Другая окружность, проходящая через точки А, В и С,
касается прямой CD. АВ = 12, ВЕ : ЕС = 4 : 5.
а) Докажите, что треугольник ACD подобен треугольнику АВЕ.
б) Найдите ВС.

Строим чертёж, анализируя каждое условие. Опишем окружность около треугольника АСD.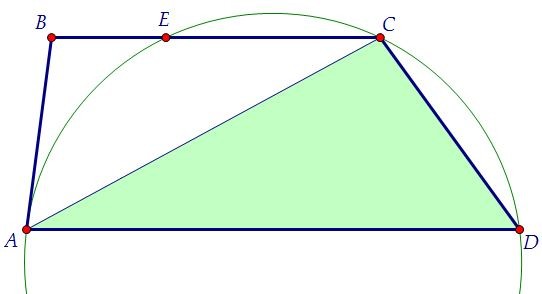



На пересечении окружности и основания ВС возникает точка Е. Зачем же она возникает?
Для того, чтобы мы увидели равнобедренную трапецию АЕСD, вписанную в окружность.



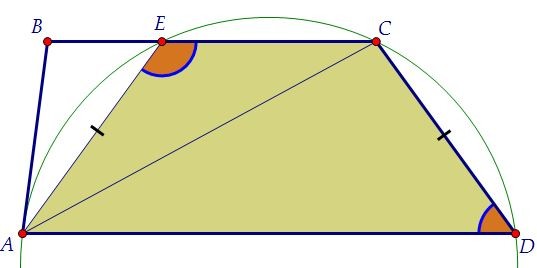Это следует из того, что сумма противоположных углов АЕС и АDC трапеции равна 180°.



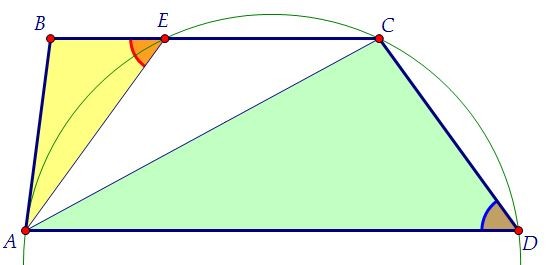Значит, угол ВЕА, смежный с углом АЕС, равен углу АDC. Пара равных углов найдена.

Проанализируем следующее условие, опишем окружность около треугольника АВС.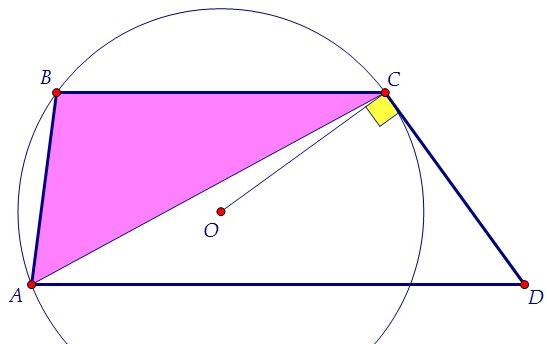



По условию CD касается окружности, а значит, CD ⊥ ОС, где т. О - центр окружности.
Угол между хордой АС и касательной CD равен половине дуги АС второй окружности.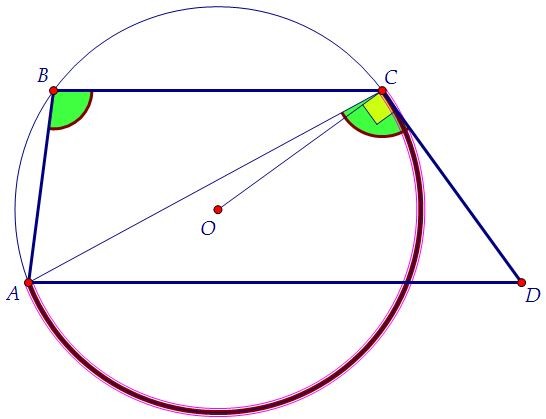



Половине этой же дуги равен вписанный угол АВС. Найдена вторая пара равных углов.
Найдя две пары равных углов, мы и доказали подобие треугольников ACD и АВЕ.



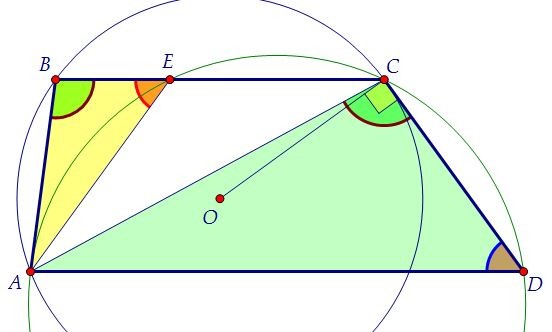Из доказанного подобия сделаем вывод о равенстве третьей пары углов, ∠ВАЕ = ∠СAD.



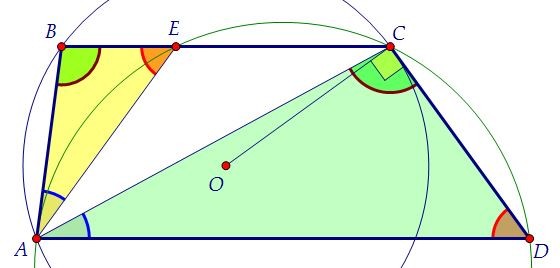Кроме того, равны дуги АЕ и СD, заключённые между параллельными прямыми ЕС и АD.



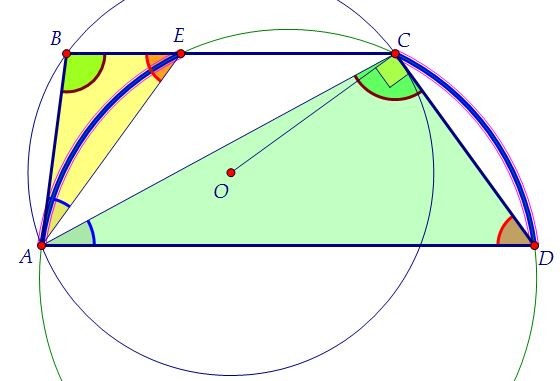Вписанный угол СAD равен половине дуги СD, а значит, угол ВАЕ равен половине дуги АЕ.
Но угол ВАЕ - это угол между хордой АЕ и прямой АВ, проходящей через конец хорды А.
Значит, прямая АВ - не просто обыкновенная прямая, а касательная ко второй окружности.
Воспользуемся свойством секущей и касательной, проведённых к окружности из точки В.



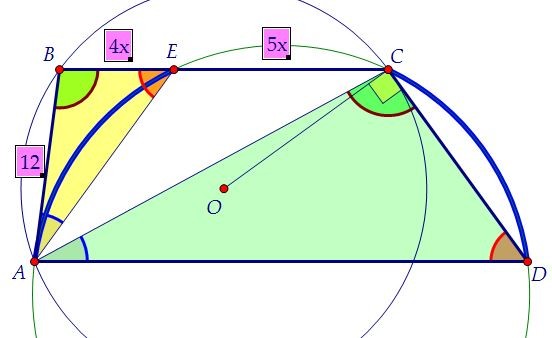ВА² = ВЕ · ВС
12² = (4х) · (9х)
36х² = 144
х² = 4
х = 2

ВС = 9х = 9 · 2 = 18

Ответ: 18

Автор: Ольга Себедаш             Просмотров: 8852