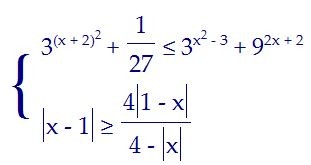Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
15(C3). Система неравенств с модулями и степенями (вар. 53)
Комментарии к этой задаче: Комментарий добавил(а): Натали Спасибо! Комментарий добавил(а): ina не поняла,почему при решении второго неравенства модуль 1-х поменялся на модуль х-1 ??? Комментарий добавил(а): Ольга Себедаш Инна, почитайте про модули. Это тождественные выражения Комментарий добавил(а): ina спасибо,Ольга,разобралась=)) Комментарий добавил(а): Ольга Себедаш Алексей, подставьте просто ноль. Комментарий добавил(а): Алексей Почему в 1 неравенстае x=0 Добавить Ваш комментарий: |