Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Две окружности с центрами О и Q пересекаются друг с другом в точках А и В,
пересекают биссектрису угла OAQ в точках С и D соответственно.
Отрезки OQ и AD пересекаются в точке Е, причем, площади
треугольников ОАЕ и QAE равны соответственно 18 и 42.
а) Докажите, что треугольники AQO и BDС подобны.
б) Найдите площадь четырехугольника OAQD.

Прежде чем приступить к пункту а), отсечём лишнее и переформулируем задачу:

Две окружности с центрами О и Q пересекаются друг с другом в точках А и В,
пересекают биссектрису угла OAQ в точках С и D соответственно.
а) Докажите, что треугольники AQO и BDС подобны.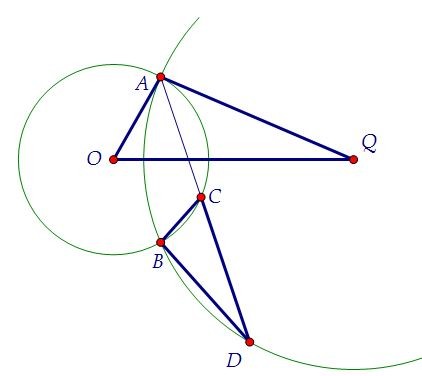



Треугольники OAQ и OВQ равны по трём сторонам. Значит, равны соответствующие
углы: ∠AQО = ∠ВQО и ∠AОQ = ∠ВОQ (и смежные с ними углы: ∠AОК = ∠ВОК).



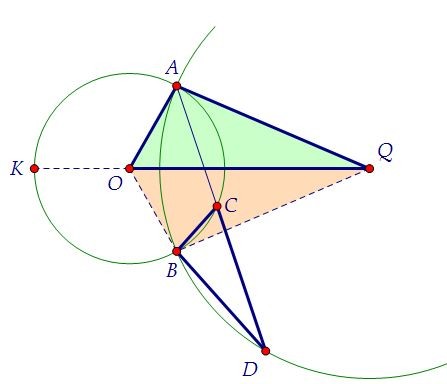Угол AQО равен половине центрального угла АQВ или половине дуги АВ.
С другой стороны, вписанный угол ВDC тоже равен половине этой дуги.



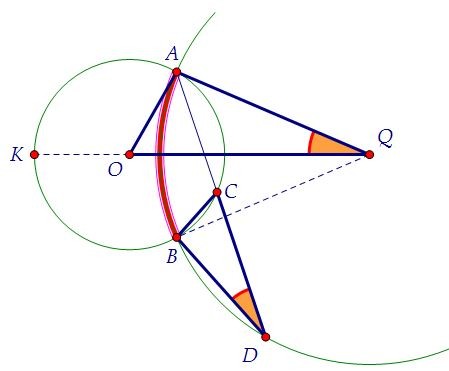Подберёмся ко второй паре равных углов (О и С) в данных треугольниках,
рассмотрим смежные с ними углы АОК и АСВ. ∠АОК центральный и равен
половине дуги АКВ. ∠АСВ вписанный и равен половине этой же дуги.



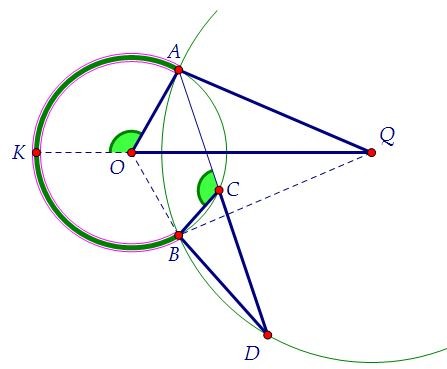Таким образом, треугольники AQO и BDС подобны по двум углам.



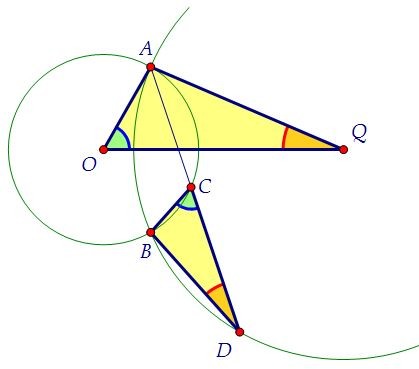Найдём площадь четырехугольника OAQD, если S_ОАЕ = 18 и S_QAE = 42.
AD - биссектриса угла А. По свойству биссектрисы ОА : QА = ОЕ : QE.



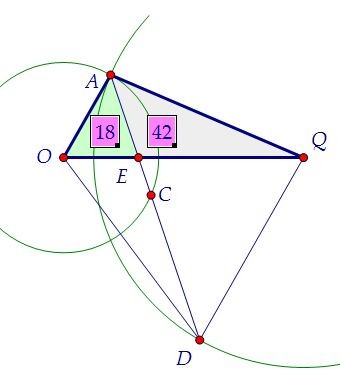S_ОАЕ : S_QAE = ОЕ : QE = 3 : 7. Поэтому ОА : QА = 3 : 7, т.е. r : R = 3 : 7.
Треугольник AQD равнобедренный, следовательно, ∠1 = ∠2 = ∠3.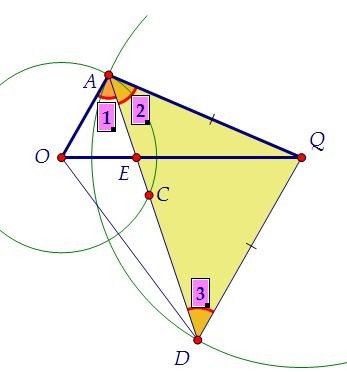



Треугольники ОАЕ и QDE подобны по двум углам. Найдём площадь QDE.



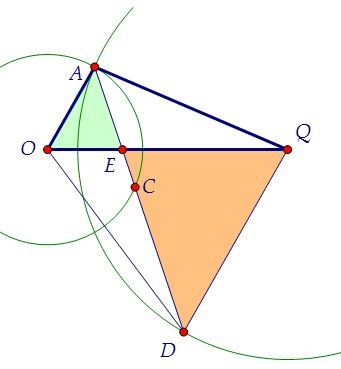Так как S_ОАЕ : S_QDE = r² : R² = 9 : 49 и по условию S_ОАЕ = 42, то S_QDE = 98.



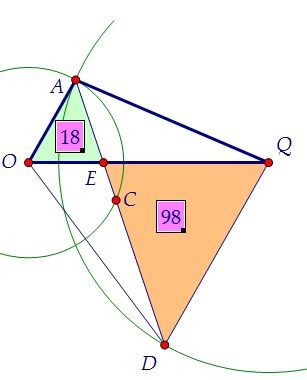S_ОDЕ : S_QDE = ОЕ : QE = 3 : 7. Так как S_QDЕ = 98, то S_ODE = 42.



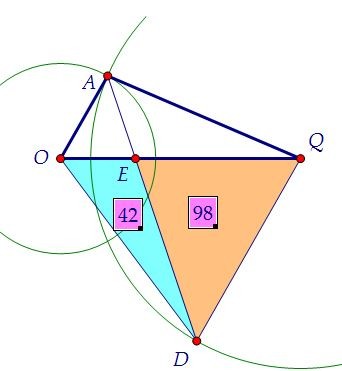В результате найдены площади четырёх треугольников, сложим их.



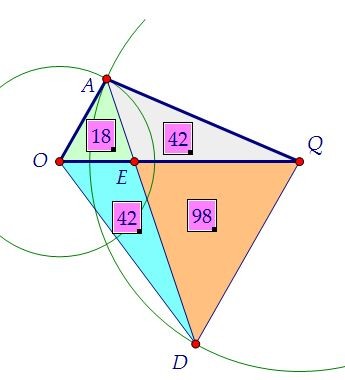Ответ: 200

Автор: Ольга Себедаш             Просмотров: 11160