Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
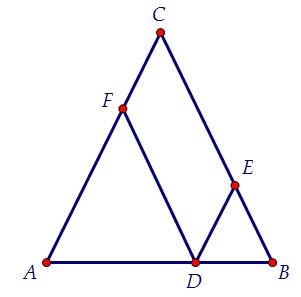
3. Периметр параллелограмма внутри равнобедренного треугольника (вар. 52)
Комментарии к этой задаче: Комментарий добавил(а): Ольга Супер! Комментарий добавил(а): Кристина Очень подробное разъяснение. Подробное и в то же время очень доступное и простое. Спасибо! Комментарий добавил(а): тим спасибо огромное Комментарий добавил(а): Добавить Ваш комментарий: |

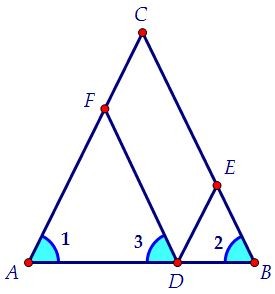 Значит, ∠1 = ∠3. Т.к. углы при основании треугольника AFD равны, то AF = FD.
Значит, ∠1 = ∠3. Т.к. углы при основании треугольника AFD равны, то AF = FD.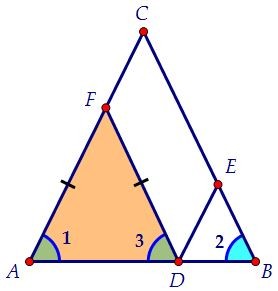 Аналогично рассуждая, получаем, что и треугольник DEB равнобедренный, DE = BE.
Аналогично рассуждая, получаем, что и треугольник DEB равнобедренный, DE = BE.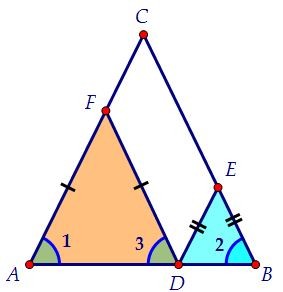 В параллелограмме FCED противоположные стороны равны: FC = DE, EC = DF.
В параллелограмме FCED противоположные стороны равны: FC = DE, EC = DF.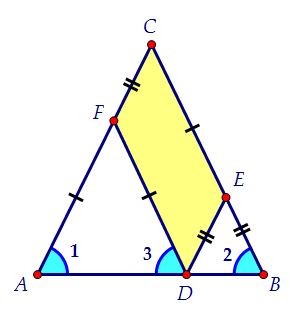 Периметр параллелограмма равен сумме его сторон: P = DF + FC + CE + ED.
Учитывая, что DF = AF и ED = EB, запишем так: P = AF + FC + CE + EB.
Получаем P = (AF + FC) + (CE + EB) = АС + СВ = 10 + 10 = 20.
Ответ: 20
Периметр параллелограмма состоит из двух зелёных и двух красных отрезков.
Периметр параллелограмма равен сумме его сторон: P = DF + FC + CE + ED.
Учитывая, что DF = AF и ED = EB, запишем так: P = AF + FC + CE + EB.
Получаем P = (AF + FC) + (CE + EB) = АС + СВ = 10 + 10 = 20.
Ответ: 20
Периметр параллелограмма состоит из двух зелёных и двух красных отрезков.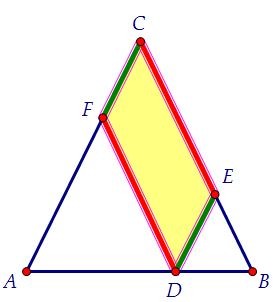 Поэтому он и равен сумме боковых сторон равнобедренного треугольника.
Поэтому он и равен сумме боковых сторон равнобедренного треугольника.