Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Площадь сечения шара плоскостью, проходящей через его центр, равна 16.
Найдите площадь сечения этого шара плоскостью, отстоящей от его центра
на расстояние, равное половине радиуса.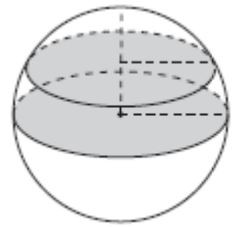

Зная площадь большого сечения, мы сможем найти радиус сечения, т.е. шара (R).
Чтобы найти площадь маленького сечения (тоже круга), надо знать его радиус (r).
S_{б. круга} = πR² = 16. Выражать ли радиус? Нет, не будем, мы пойдём другим путём.
Найдём, как связаны оба радиуса (R : r), а затем найдём отношение площадей.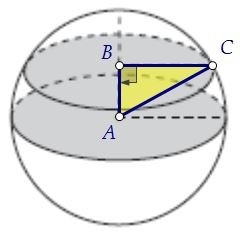



Расстояние между сечениями в два раза меньше радиуса, т. е. АС = 2·АВ.
Из треугольника АВС по т. Пифагора найдём маленький радиус, т.е. ВС.
ВС² = АС² - АВ² = (2·АВ)² - АВ² = 4АВ² - АВ² = 3АВ²,        ВС = АВ√3.

Итак, R = 2AB, r = АВ√3, отношение радиусов R : r = 2 : √3.
Значит, отношение площадей кругов S_б. : S_м. = 4 : 3.
По условию S_б. = 16, получаем 16 : S_м. = 4 : 3.
Отсюда S_м. = 12.

Ответ: 12

Автор: Ольга Себедаш             Просмотров: 68781