Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В выпуклом четырехугольнике KLMN точки А, В, С, D – средины сторон KL, LM, MN, NK
соответственно. Известно, что KL = 3. Отрезки АС и BD пересекаются в точке О.
Площади четырехугольников KAOD, LAOB и NDOC равны соответственно 6, 6 и 9.
а) Докажите, что площади четырехугольников MCOB и NDOC равны
б) Найдите длину отрезка MN

Остановимся на первой фразе и рассмотрим стандартную ситуацию - середины сторон
произвольного четырёхугольника всегда являются вершинами параллелограмма.



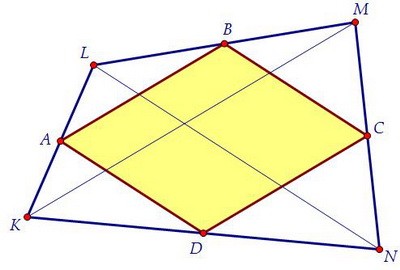Нам важен этот факт и факт равенства площадей четырёхугольников KAOD и LAOB.



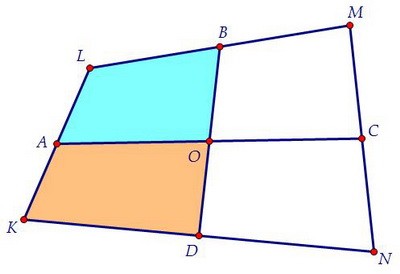Каждый четырёхугольник состоит из двух треугольников. Площади треугольников
АВО, ADO равны, т.к. АО - медиана треугольника AВD (ВО = ОD).



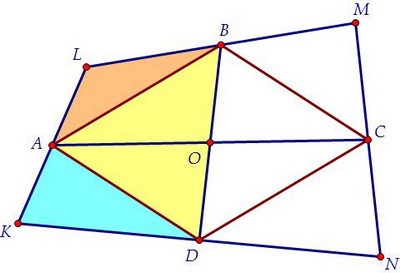Следовательно, равны площади треугольников ALB и AKD. У этих треугольников
равны основания AL и AK, а значит, и высоты, проведённые к этим основаниям.
Расстояния от точек К и L до прямой BD равны, отсюда следует, что KL || BD.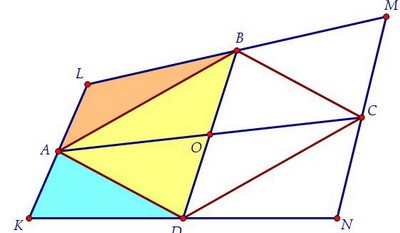



Если через точку М провести прямую МР, параллельную прямым KL и BD, то
отрезки KD и DР окажутся равными по теореме Фалеса. Поэтому точка Р
совпадёт с точкой N и MN || KL || BD. Следовательно, S_BMC = S_DNC.



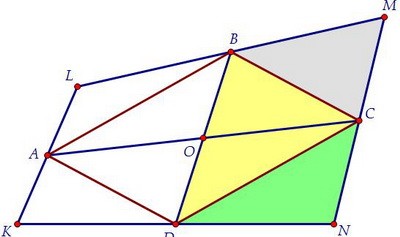А учитывая, что S_BОC = S_DОC, получаем равенство площадей MCOB и NDOC.

Для ответа на второй вопрос уберём лишнее и оставим лишь трапецию KLMN
и её среднюю линию ВD. Известно, что S_KLBD = 12, S_DBMN = 18 и KL = 3.



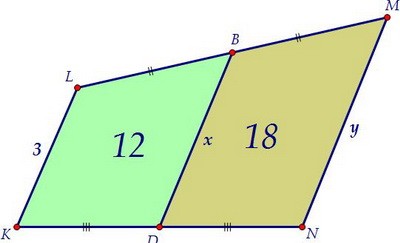Обозначим BD = x и MN = y. Высоты двух трапеций на рисунке равны, поэтому
площади трапеций пропорциональны суммам их оснований. Запишем это:







Кроме того, верно равенство 2х = y + 3, т.к. ВD - средняя линия трапеции KLMN.
Подставим в это равенство x = 2y - 9 и получим 2(2y - 9) = y + 3. Отсюда y = 7.

Ответ: 7

Автор: Ольга Себедаш             Просмотров: 14368