Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
12(B13). Найти диаметр основания цилиндра, если дана боковая поверхность (вар. 49)
Комментарии к этой задаче: Комментарий добавил(а): Артур А общее формула нахождение диаметра цилиндра? Она имеет лишь такое произведение? Или есть иное? Комментарий добавил(а): Добавить Ваш комментарий: |

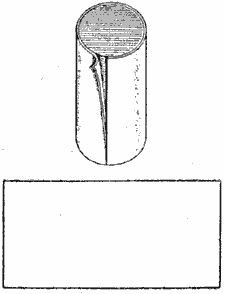 При этом получим обыкновенный прямоугольник. Одно из его измерений - высота цилиндра.
Второе измерение - длина окружности основания цилиндра. Она равна 2π·R = π·(2R) = π·D.
При этом получим обыкновенный прямоугольник. Одно из его измерений - высота цилиндра.
Второе измерение - длина окружности основания цилиндра. Она равна 2π·R = π·(2R) = π·D.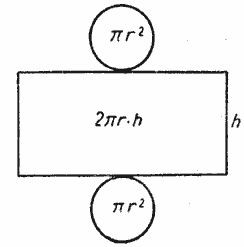 На рисунке изображена полная развёртка цилиндра, но нас интересует только прямоугольник.Площадь прямоугольника (боковая поверхность) равна (π·D)·Н. По условию она равна 56π. Получаем (π·D)·Н = 56π. Отсюда D·Н = 56. Учтём теперь, что по условию высота равна 7. D·7 = 56. Отсюда находим диаметр D = 8.Ответ: 8
Можно поступить и так. В формулу боковой поверхности цилиндра Sбок. = 2π·R·Hподставить площадь 56π и высоту 7, получим 56π = 2πR·7, 56 = 2R·7, 8 = 2R = D.
На рисунке изображена полная развёртка цилиндра, но нас интересует только прямоугольник.Площадь прямоугольника (боковая поверхность) равна (π·D)·Н. По условию она равна 56π. Получаем (π·D)·Н = 56π. Отсюда D·Н = 56. Учтём теперь, что по условию высота равна 7. D·7 = 56. Отсюда находим диаметр D = 8.Ответ: 8
Можно поступить и так. В формулу боковой поверхности цилиндра Sбок. = 2π·R·Hподставить площадь 56π и высоту 7, получим 56π = 2πR·7, 56 = 2R·7, 8 = 2R = D.