Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра
равны 13. Найдите площадь боковой поверхности этой пирамиды. 

Боковая поверхность правильной шестиугольной пирамиды состоит из шести равных
равнобедренных треугольников, основания которых равны 10, а боковые стороны - 13.



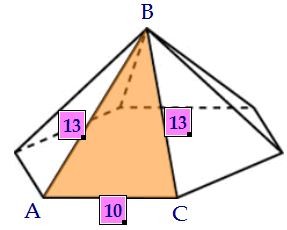Чтобы найти площадь одной боковой грани, надо знать высоту, проведённую к основанию.
Для этого возьмём середину основания D, AD = DC = 5. Медиана ВD является и высотой.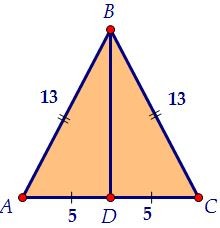



Из прямоугольного треугольника АВD с гипотенузой 13 и катетом 5 находим второй катет 12.



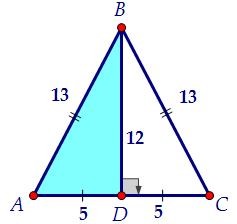По теореме Пифагора BD² = AB² - AD² = 13² - 5² = 169 - 25 = 144. BD = √144 = 12.
Площадь треугольника равна половине произведения основания на высоту.
S_ABC = 0,5 · AC · BD = 0,5 · 10 · 12 = 5 · 12 = 60
Чтобы найти площадь боковой поверхности, надо умножить 60 на 6. S_бок. = 360.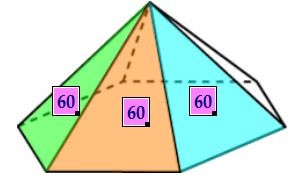



Ответ: 360

Автор: Ольга Себедаш             Просмотров: 146671