Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Через вершины В и С треугольника АВС проходит окружность, пересекающая
стороны АВ и АС соответственно в точках К и М.
а) Доказать, что треугольники АВС и АМК подобны.
б) Найти МК и АМ, если АВ = 2, ВС = 4, СА = 5, АК = 1.

Центр окружности, проходящей через В и С, лежит на серединном перпендикуляре к ВС.



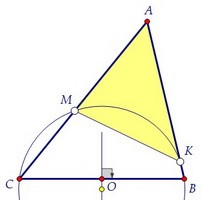
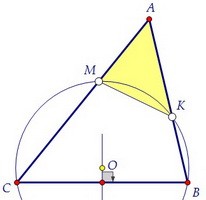
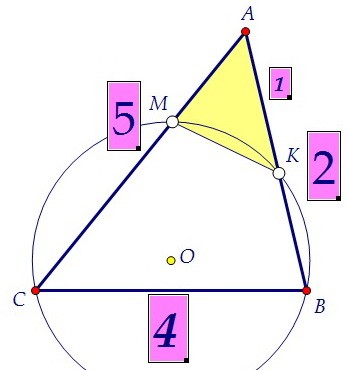
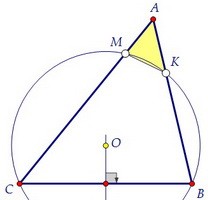Треугольники АВС и АМК подобны по двум углам. Угол САВ общий, а ∠АМК = ∠АВС.



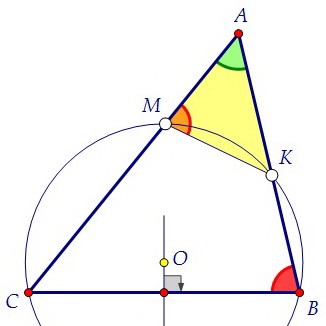Почему же? Дело в том, что каждый из них вместе с углом СМК даёт в сумме 180°.



Углы АМК и СМК смежные, а углы АВС и СМК - противоположные углы вписанного
в окружность четырёхугольника СМКВ (это свойство тоже надо уметь доказывать).

Замечу, что доказав подобие треугольников, мы легко сделаем вывод о том, что



Отсюда АМ · АС = АК · АВ. Мы доказали заодно свойство секущих к окружности.

Учитывая данные задачи, найдём коэффициент подобия, он равен АК:АС = 1:5.



МК:ВС = 1:5                              АМ:АВ = 1:5
МК:4 = 0,2                                АМ:2 = 0,2
МК = 0,8                                   АМ = 0,4

Ответ: 0,8; 0,4

Автор: Ольга Себедаш             Просмотров: 48028