|
Найдите все значения параметра а, при каждом из которых уравнение
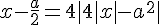 имеет ровно три корня. имеет ровно три корня.
Вынесем четвёрку за знак внешнего модуля в правой части:
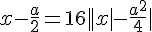
^2|) После этого сделаем очевидную замену параметра, избавившись от дробей:
После этого сделаем очевидную замену параметра, избавившись от дробей:
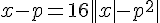 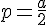 Справа находится чётная функция, график симметричен относительно оси OY,
расположен не ниже оси ОХ и пересекает ось абсцисс в двух точках х = ±р2.
На луче [р2; +∞) функция возрастает, на отрезке [0; р2] функция убывает.
Это нетрудно увидеть, раскрыв модули. С учётом симметричности получим,что на луче (-∞; -р2] функция убывает, на отрезке [-р2; 0] - возрастает.
Справа находится чётная функция, график симметричен относительно оси OY,
расположен не ниже оси ОХ и пересекает ось абсцисс в двух точках х = ±р2.
На луче [р2; +∞) функция возрастает, на отрезке [0; р2] функция убывает.
Это нетрудно увидеть, раскрыв модули. С учётом симметричности получим,что на луче (-∞; -р2] функция убывает, на отрезке [-р2; 0] - возрастает.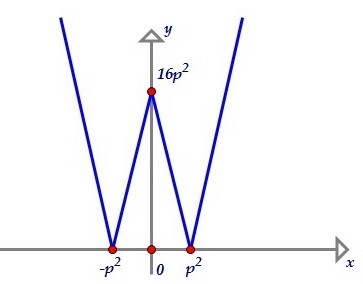 Конечно, можно применить и законы построения графиков, содержащих модули.
Левая часть уравнения представляет из себя линейную возрастающую функцию.
Конечно, можно применить и законы построения графиков, содержащих модули.
Левая часть уравнения представляет из себя линейную возрастающую функцию.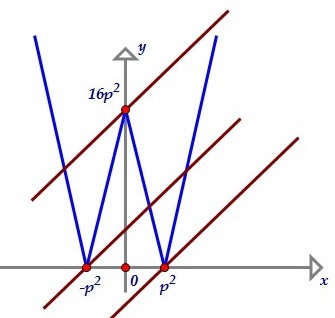 Прямая пересечёт нашу функцию в нечётном числе точек, только если
пройдёт через точки излома: (-р2; 0), (р2; 0) или (0; 16р2). Иначе она пересечёт ломаную в двух точках или четырёх точках или вообще не пересечёт.
Прямая пересечёт нашу функцию в нечётном числе точек, только если
пройдёт через точки излома: (-р2; 0), (р2; 0) или (0; 16р2). Иначе она пересечёт ломаную в двух точках или четырёх точках или вообще не пересечёт.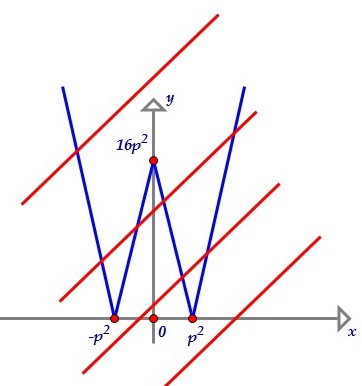 Итак, условия х = ±р2 и х = 0 являются необходимыми (но не достаточными).
Отсюда намечаем план решения:
1) Подставляем в уравнение х = ±р2 и х = 0 и находим значения параметра, при которых эти числа являются корнями уравнения.
2) Проверяем каждое найденное значение параметра, т.е. убеждаемся, что корней будет именно три, а не один.
* Заметим, что наличие графика и здравый смысл подсказывают, что нас устроят
именно прямые, проходящие через точки (-р2; 0) или (0; 16р2), и не устроит прямая, проходящая через (р2; 0). Ответ предсказуем.
..... Продолжение следует.....
Итак, условия х = ±р2 и х = 0 являются необходимыми (но не достаточными).
Отсюда намечаем план решения:
1) Подставляем в уравнение х = ±р2 и х = 0 и находим значения параметра, при которых эти числа являются корнями уравнения.
2) Проверяем каждое найденное значение параметра, т.е. убеждаемся, что корней будет именно три, а не один.
* Заметим, что наличие графика и здравый смысл подсказывают, что нас устроят
именно прямые, проходящие через точки (-р2; 0) или (0; 16р2), и не устроит прямая, проходящая через (р2; 0). Ответ предсказуем.
..... Продолжение следует..... Автор: Ольга Себедаш Просмотров: 11585
|

 Конечно, можно применить и законы построения графиков, содержащих модули.
Левая часть уравнения представляет из себя линейную возрастающую функцию.
Конечно, можно применить и законы построения графиков, содержащих модули.
Левая часть уравнения представляет из себя линейную возрастающую функцию. Прямая пересечёт нашу функцию в нечётном числе точек, только если
пройдёт через точки излома: (-р2; 0), (р2; 0) или (0; 16р2). Иначе она пересечёт ломаную в двух точках или четырёх точках или вообще не пересечёт.
Прямая пересечёт нашу функцию в нечётном числе точек, только если
пройдёт через точки излома: (-р2; 0), (р2; 0) или (0; 16р2). Иначе она пересечёт ломаную в двух точках или четырёх точках или вообще не пересечёт. Итак, условия х = ±р2 и х = 0 являются необходимыми (но не достаточными).
Отсюда намечаем план решения:
1) Подставляем в уравнение х = ±р2 и х = 0 и находим значения параметра, при которых эти числа являются корнями уравнения.
2) Проверяем каждое найденное значение параметра, т.е. убеждаемся, что корней будет именно три, а не один.
* Заметим, что наличие графика и здравый смысл подсказывают, что нас устроят
именно прямые, проходящие через точки (-р2; 0) или (0; 16р2), и не устроит прямая, проходящая через (р2; 0). Ответ предсказуем.
..... Продолжение следует.....
Итак, условия х = ±р2 и х = 0 являются необходимыми (но не достаточными).
Отсюда намечаем план решения:
1) Подставляем в уравнение х = ±р2 и х = 0 и находим значения параметра, при которых эти числа являются корнями уравнения.
2) Проверяем каждое найденное значение параметра, т.е. убеждаемся, что корней будет именно три, а не один.
* Заметим, что наличие графика и здравый смысл подсказывают, что нас устроят
именно прямые, проходящие через точки (-р2; 0) или (0; 16р2), и не устроит прямая, проходящая через (р2; 0). Ответ предсказуем.
..... Продолжение следует.....