|
Касательные CA и CB к окружности образуют угол ACB, равный 122°.
Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.
Градусная мера дуги АВ окружности - это градусная мера центрального угла АОВ.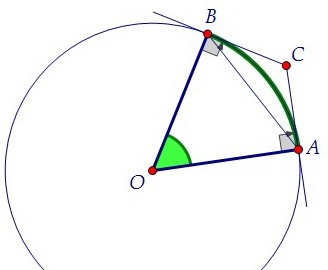
Чтобы найти величину угла АОВ, рассмотрим четырёхугольник ОВСА. Заметим, что
касательная перпендикулярна радиусу окружности, проведённому в точку касания.
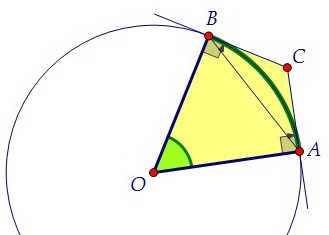Таким образом, в четырёхугольнике ОВСА ∠ОАС = ∠ОВС = 90°, а ∠ACB = 122°.
Сумма углов четырёхугольника равна 360°. Зная три угла, находим четвёртый:
∠АОВ = 360° - 90° - 90° - 122° = 180° - 122° = 58°.
Ответ: 58°
Возможен и другой путь. Рассмотрим треугольник АВС, он равнобедренный, т.к. отрезки касательных, проведённых из точки С к окружности, равны, СВ = СА.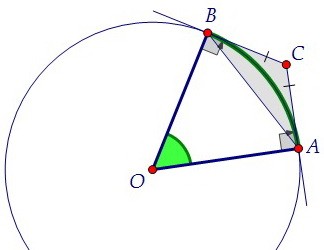
В равнобедренном треугольнике углы при основании равны, найдём эти углы. ∠АВС = ∠ВАС = (180° - 122°) : 2 = 29°.
Треугольник АОВ тоже равнобедренный, боковые стороны равны как радиусы.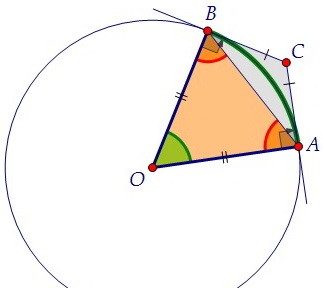
∠ОАВ = ∠ОАС - ∠ВАС = 90° - 29° = 61°.
∠ОВА = ∠ОАВ = 61° (можно его найти аналогично).
∠АОВ = 180° - ∠ОАВ - ∠ОВА = 180° - 61° - 61° = 180° - 122° = 58°. Автор: Ольга Себедаш Просмотров: 42411
|
