Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Найдите высоту треугольника АВС, опущенную на сторону ВС,
если стороны квадратных клеток равны √5.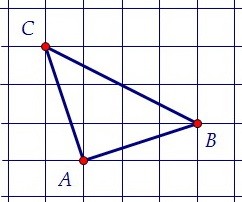

Легко заметить, что перед нами равнобедренный треугольник, т.к. АВ = АС.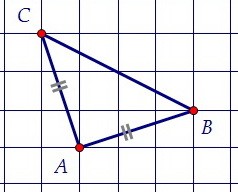



Медиана равнобедренного треугольника, опущенная к основанию, является высотой.



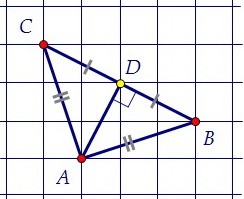Возьмём середину основания - точку D. АD - медиана, и значит, АD - высота.

Длину отрезка АD найдём как гипотенузу в прямоугольном треугольнике АКD.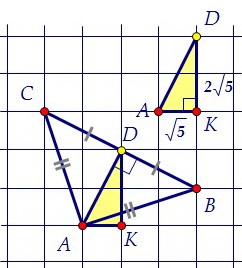



АК = √5;      КD = 2√5;      АD² = АК² + DK² = (√5)² + (2√5)² = 5 + 20 = 25;
AD = 5.

Ответ: 5

Ещё можно заметить, что медиана и высота АD треугольника равна половине основания.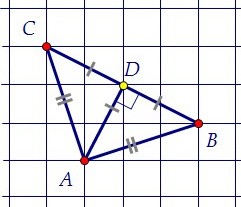



Таким свойством, кстати, обладают только прямоугольные треугольники.
Найдём основание ВС как гипотенузу прямоугольного треугольника ВСР.



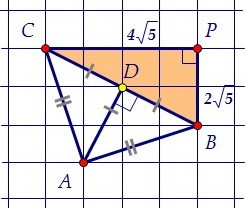ВР = 2√5;    СР = 4√5;    ВС² = ВР² + СР² = (2√5)² + (4√5)² = 20 + 80 = 100;
ВС = 10;      AD = 5.

Вернёмся к жёлтому прямоугольному треугольнику. Замечу, что теорему Пифагора
легче использовать, приняв сторону клетки за 1. В этом случае катеты равны 1 и 2,
а гипотенуза равна √5. Но это число надо умножить на √5 - коэффициент подобия.
Таким образом, мы и получим 5.

Автор: Ольга Себедаш             Просмотров: 59798