Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
12(B13). В сосуд, имеющий форму правильной треугольной призмы, налили воду (вар. 47)
Комментарии к этой задаче: Комментарий добавил(а): валерий спасибо) ты очень выручили Комментарий добавил(а): Настя Большое вам спасибо) Комментарий добавил(а): Ира Большое спасибо Комментарий добавил(а): Евгений Интересно Комментарий добавил(а): Максим Спасибо очень помогло Комментарий добавил(а): Александр Спасибо Комментарий добавил(а): Вика Это каким образом определили? "Сторона основания нового широкого сосуда в три раза больше стороны старого узкого. Значит, площадь основания нового в 32 = 9 раз больше площади основания старого." Комментарий добавил(а): HEESETIED Всем привет Здравствуйте, проживаю в Российской глубинке ( В городе Димитровград. Нужен мощный и недорогой ноутбук стоимостью до 40 000 руб. Гуглил - самые шоколадные предложения, естественно в Москве. Но чет страшновато посылать деньги, а потом ждать ноут ((( Может кто знает, какие магазы высылают такой товар наложкой ? Из приличных , пока нагуглил только магазин ТОТЕМО, но хочется еще посравнивать цены с другими, которые высылают наложенным платежом... P.S. всякие мвидео, эльдарады - пожалуйста, не предлагайте, там цены космос.... Комментарий добавил(а): annaned Комментарий добавил(а): Nemezida Комментарий добавил(а): ant.wrightt О проекте Жилой комплекс «Вавилов ДОМ» расположен в престижном Академическом районе ЮЗАО Москвы, в 10 минутах ходьбы от станции метро «Академическая». Проект бизнес-класса представляет собой два 19 этажных корпуса, объединенных первым этажом, где располагаются просторные входные группы и объекты коммерческой инфраструктуры. Дома построены по монолитной технологии, отделка фасадов выполнена испанскими панелями Faveton из натуральной терракотовой глины. Современные лифты с прямым доступом к подземному паркингу, закрытая охраняемая территория, благоустроенный "двор без машин" с детскими площадками и зонами отдыха обеспечат комфорт и безопасность будущим жителям. Благоприятная экологическая ситуация района ЖК «Вавилов ДОМ» - ближайшая парковая зона находится всего в 400 метрах. Около полутора километров до самых популярных мест отдыха горожан – Воробьевых гор и Ленинских гор. Преимущества ЖК «Вавилов ДОМ»: Благоприятная экология – жилой комплекс недалеко от природных заказников, источников свежего воздуха и находится на удалении от шумных автомагистралей; Престижный район. Интеллигентное окружение, задаваемое действующими вокруг вузами, НИИ и научными лабораториями; Близость к центру и хорошая транспортная доступность – рядом находится станция метро и развязка ТТК. Трамвайные и автобусные маршруты; Развитая социальная инфраструктура района; Уникальные видовые характеристики квартир; Отделка WHITE BOX; Двухуровневый подземный паркинг на 280 машиномест. Жилой комплекс располагается по адресу: г. Москва, ул. Вавилова, стр. 27-31.   Срок сдачи: 2-й квартал 2019г. Подробности по телефону: +7 (925) 315-65-68!  Звоните с 9-00 до 21-00 с понедельника по воскресенье. Комментарий добавил(а): Alndreyned Комментарий добавил(а): Juliyshort Комментарий добавил(а): Antonned Комментарий добавил(а): Alexeyned Комментарий добавил(а): clavaned Комментарий добавил(а): Alexeyned Комментарий добавил(а): clavaned Комментарий добавил(а): Antoniodow Комментарий добавил(а): RobertCip Комментарий добавил(а): andreined Комментарий добавил(а): WilliamGurse Комментарий добавил(а): JeffreyKax Комментарий добавил(а): RachaelFax Добавить Ваш комментарий: |
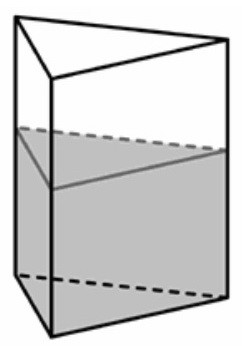
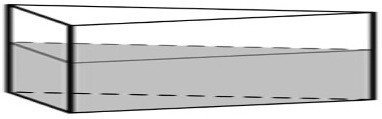Объём налитой в сосуд жидкости не меняется, её не добавляют и не выливают.
А объём, как известно, равен произведению площади основания на высоту.
Поэтому если площадь основания увеличилась в 9 раз, то высоте пришлось при этом в 9 раз уменьшиться.
Высота жидкости была равна 18 см, а стала равна 18 : 9 = 2 см.Ответ: 2
Для любителей формул можно расписать подробнее:
Vстарый = Sстарая · Hстарая
Vновый = Sновая · Hновая
Vновый = 9·Sстарая · Hновая
Так как Vстарый = Vновый, то Hстарая = 9 · Hновая
18 = 9 · Hновая
Hновая = 2