Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
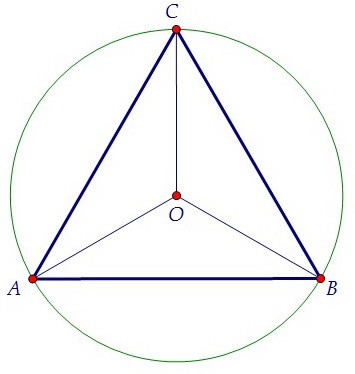
6. Найти радиус описанной около правильного треугольника окружности (вар. 47)
Комментарии к этой задаче: Комментарий добавил(а): Серафима Здравствуйте, спасибо за подробное описание задачи.У Вас во втором способе решения ошибка, АВ^2 = 3R^2 АВ^2 = R√3 не убрана вторая степень. Комментарий добавил(а): Ольга Себедаш Серафима, спасибо! Поправила Комментарий добавил(а): Полина Можно также решить через теорему синусов. Она связывает сторону, угол и 2 радиуса описанной окружности. Вот это действительно самый короткий способ в одно действие) Комментарий добавил(а): Виктория Спасибо! Комментарий добавил(а): Neooreale Добавить Ваш комментарий: |

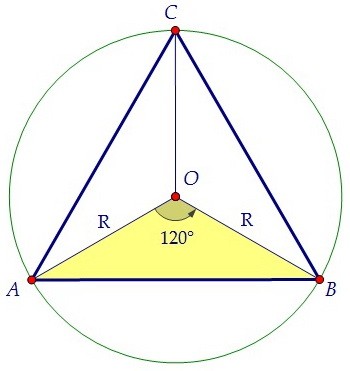 Этот факт легко подтверждается с помощью теоремы косинусов, записанной для стороны АВ.
АВ2 = R2 + R2 - 2·R·R·cos120°
АВ2 = 2R2 - 2R2·(-0,5)
АВ2 = 2R2 + R2
АВ2 = 3R2
АВ = R√3
√3 = R√3
R = 1
Способ 3 (универсальный для правильных треугольников).
Продлим отрезок СО до пересечения с АВ в точке Е. СЕ - высота треугольника АВС.
Этот факт легко подтверждается с помощью теоремы косинусов, записанной для стороны АВ.
АВ2 = R2 + R2 - 2·R·R·cos120°
АВ2 = 2R2 - 2R2·(-0,5)
АВ2 = 2R2 + R2
АВ2 = 3R2
АВ = R√3
√3 = R√3
R = 1
Способ 3 (универсальный для правильных треугольников).
Продлим отрезок СО до пересечения с АВ в точке Е. СЕ - высота треугольника АВС.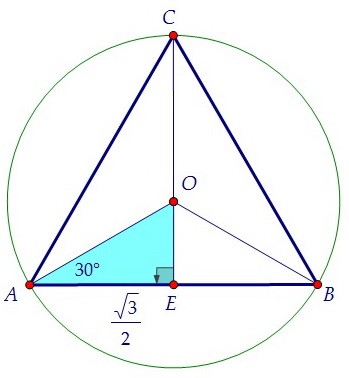 Рассмотрим прямоугольный треугольник АОЕ с углом 30° и катетом АЕ = 0,5·АВ.
Мы воспользовались тем, что СЕ - медиана треугольника и АО - биссектриса.
По определению косинуса острого угла прямоугольного треугольника:
Рассмотрим прямоугольный треугольник АОЕ с углом 30° и катетом АЕ = 0,5·АВ.
Мы воспользовались тем, что СЕ - медиана треугольника и АО - биссектриса.
По определению косинуса острого угла прямоугольного треугольника: