|
Найдите все значения параметра а, при каждом из которых уравнение
x|x + 2a| + 1 - a = 0 имеет единственное решение.
Раскроем модуль на двух лучах.
Если x < -2a, то x2 + 2ax + (a - 1) = 0.
Если x ≥ -2a, то x2 + 2ax + (1 - a) = 0.
Дискриминант первого уравнения положителен всегда, уравнение имеет два корня.
Возможны следующие случаи расположения параболы относительно точки х = -2а: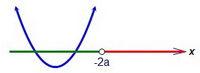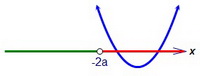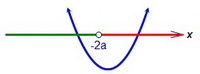  
В первом случае на левом луче есть уже два корня, этот случай нам неинтересен.
Необходимым для расположения корней правее -2а является условие f(-2a) > 0.
f(-2a) = (-2a)2 + 2a(-2a) + (a - 1) = а - 1 > 0; a > 1 При этом первая координата вершины параболы -а расположена правее точки -2а. Вот наш второй случай:
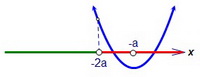Рассмотрим второе уравнение и обозначим его левую часть g(x). Заметим, что g(-2а) = (-2a)2 + 2a(-2a) + (1 - а) = 1 - а < 0 при a > 1. Заметим к тому же, что первые координаты вершин обеих парабол совпадают. Новый рисунок:
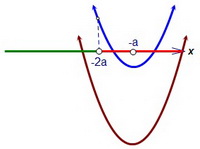Очевидно, что второе уравнение имеет единственный корень на правом луче.
Итак, при a > 1 условие задачи выполнено. Второй случай нами рассмотрен.
Для третьего случая необходимо условие f(-2a) < 0, т.е. a < 1. Разобьём его
на два: 1) a < 0 и 2) 0 < a < 1. Первая координата вершины обеих парабол
х = -а при a < 0 расположена левее точки х = -2а, а при 0 < a < 1 - правее.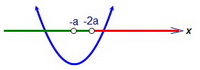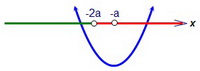 
Т.к. f(-2a) < 0, то g(-2a) > 0. В первом подслучае (-а < -2a) второе уравнение не имеет корней на правом луче (или совсем их не имеет), что нас устраивает. 
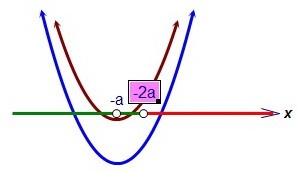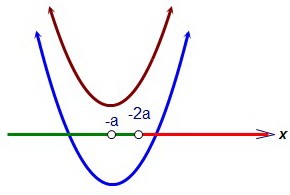Во втором подслучае (-а > -2a), учитывая, что g(-2a) > 0, потребуем, чтобы
второе уравнение не имело корней вовсе, иначе условие не выполнится.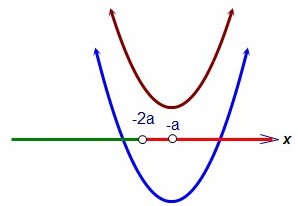
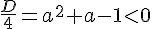
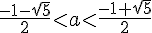Так как 0 < a < 1, то получаем в пересечении
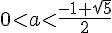Добавим к этому интервалу два полученных выше луча a < 0 и а >1
и проверим отдельно два пропущенных значения а - ноль и единицу.
Если а = 0, то уравнение x|x| + 1 = 0 имеет единственный корень -1.
Если а = 1, то уравнение x|x + 2| = 0 имеет два корня -2 и 0.
Ответ: ; (1; +\infty)) Автор: Ольга Себедаш Просмотров: 15431
|
