Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

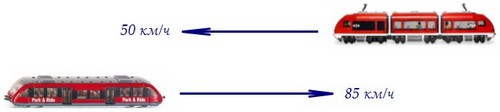
По двум параллельным железнодорожным путям друг навстречу другу следуют скорый
и пассажирский поезда, скорости которых равны соответственно 85 км/ч и 50 км/ч.
Длина пассажирского поезда равна 600 метрам. Найдите длину (м) скорого поезда,
если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам.

Переформулируем задачу. Остановим пассажирский и заставим скорый мчаться
с общей скоростью обоих поездов: 50 + 85 = 135 км/ч. Тогда скорому поезду
надо промчаться мимо неподвижного состава длиной 600 метров = 0,6 км.



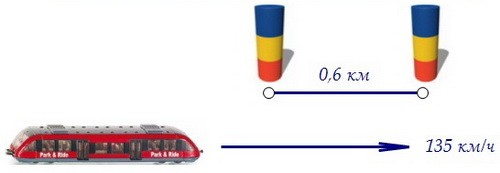В начальный момент времени машинист скорого поезда поравнялся с машинистом
пассажирского поезда. Только здесь мы начинаем засекать время и путь скорого.

     

В промежуточный момент времени машинист скорого миновал пассажирский поезд,
проехав пока 0,6 км. Но пока только машинист его миновал. Цель не достигнута.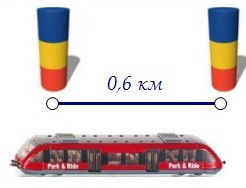

                                  

В конечный момент времени машинист скорого проехал ещё и длину собственного
поезда (х километров), чтобы целиком миновать пассажирский поезд.

                                       

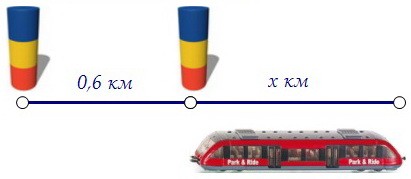Весь путь скорого поезда получился равным (х + 0,6) км, скорость его 135 км/час.
Время переведём в часы. 36 сек. = 36 : 3600 = 0,01 часа, т.к. в часе 3600 секунд.
Итак, за 0,01 часа со скоростью 135 км/час ускоренный поезд прошёл (х + 0,6) км.

135 · 0,01 = х + 0,6
х + 0,6 = 1,35
х = 0,75

Таким образом, длина скорого поезда равна 0,75 километра или 750 метров.

Ответ: 750

Автор: Ольга Себедаш             Просмотров: 22072