Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
6. Найти хорду окружности по радиусу и вписанному углу (вар. 46)
Комментарии к этой задаче: Комментарий добавил(а): WilliamNax Здравствуйте! Меня зовут Елена. Занимаюсь созданием милых и прекрасных куколок Блайз (Blythe) Хочу предложить на Ваш суд этих радующих взгляд созданий. Все подробности на моём сайте blythedom.com -Приедет красиво и надёжно упакованной -И ещё один важный момент - куколка не для активных детских игр!!! ( Вернее сказать - покупка для детей на усмотрение родителей:). Все же больше для эстетики и для девочек по старше :)) ) -Кукла тяжёлая со своим собственным глазным механизмом и возможностью переключать 4 пары глаз . -Тело шарнирное!!! Вся одежда в миниатюре 1/6 я шью исключительно сама. Ботиночки шью вручную сама. -Глаза стекло с эффектом мерцания я так же изготавливаю сама. -Сделан карвинг( перепилен нос, губы, щечки, подбородок ). Поднят «взгляд», сделаны «спящие веки». Замена ресниц на реалистичные. Мэйк выполнен проф.пастелью, закреплён спец.средством. -Приедет в аутфите, что представлен на кукле. Больше фотографий по запросу . Я никогда не использую фотошоп для редактирования фотографий! Однако -Цвет товара может незначительно отличаться из- за разницы цветопередачи монитора Ваших устройств!!! Комментарий добавил(а): Комментарий добавил(а): Комментарий добавил(а): Добавить Ваш комментарий: |
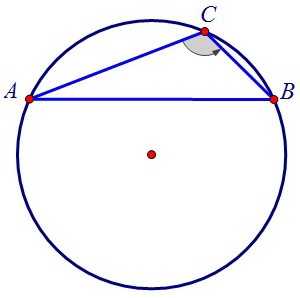
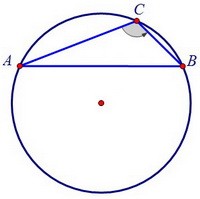
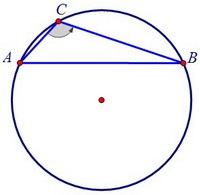
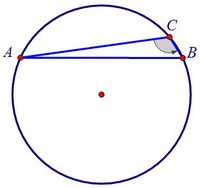Но при данном радиусе и данном вписанном угле С хорда АВ остаётся неизменной.
Найти хорду можно из равнобедренного треугольника ОАВ, где ОА = ОВ = R = √3.
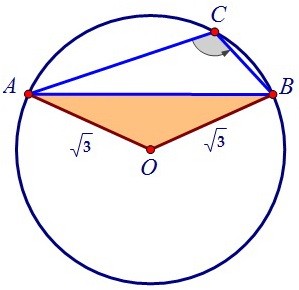Для этого необходимо знать ∠АОВ, а он равен красной дуге, на которую опирается.
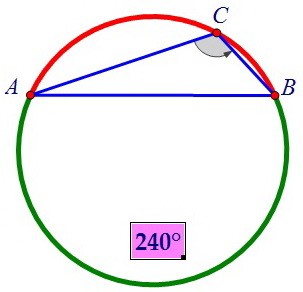Красная дуга дополняет зелёную до 360°, а зелёная равна 2 · 120° = 240° (вписанный угол равен половине дуги, на которую он опирается). Итак, ∠АОВ = 360° - 240° = 120°.
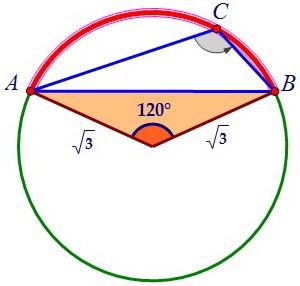Применим теорему косинусов для поиска стороны АВ в треугольнике АОВ.
АВ2 = R2 + R2 - 2·R·R·cos120°
АВ2 = 2R2 - 2R2·(-0,5)
АВ2 = 2R2 + R2
АВ2 = 3R2
АВ = R√3
АВ = √3·√3 = 3
Ответ: 3
1. В равнобедренном треугольнике с углом 120° основание в √3 раз больше боковой стороны.
2. Возможно, Вам кажется, что ∠АОВ = ∠АСВ, и так будет всегда. Проверьте при ∠АСВ = 130°.
3. Если Вы любите формулы и знаете теорему синусов, то можете найти хорду АВ по-другому:
