Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
3. Нахождение средней линии трапеции по клеточкам (вар. 46)
Комментарии к этой задаче: Комментарий добавил(а): Женя 2 способ такой крутой))) Комментарий добавил(а): Роман Можно еще другим способом - найти диагональ клетки и посчитать. Комментарий добавил(а): Комментарий добавил(а): Добавить Ваш комментарий: |

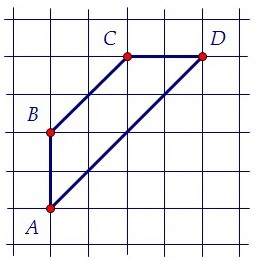
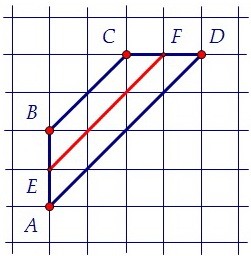 В данной трапеции боковыми сторонами являются АВ и СD, E и F - середины боковых сторон.
Длина средней линии EF состоит из трёх диагоналей клеток. Найдём длину одной диагонали.
В данной трапеции боковыми сторонами являются АВ и СD, E и F - середины боковых сторон.
Длина средней линии EF состоит из трёх диагоналей клеток. Найдём длину одной диагонали.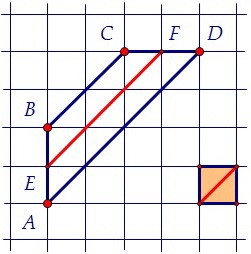 Гипотенуза прямоугольного равнобедренного треугольника в √2 раз больше катета.
Если Вы помните об этом, просто умножьте √2 на √2. Длина диагонали равна двум.
Если Вы об этом не помните, то примените теорему Пифагора: х2 = (√2)2 + (√2)2.
х2 = 2 + 2 = 4. Отсюда так или иначе находим, что диагональ клетки равна двум.
Осталось длину диагонали умножить на три. Средняя линия трапеции равна шести.
Ответ: 6
Если Вам нравится применять формулы, то воспользуемся тем, что средняя линия трапеции равна полусумме оснований.
Гипотенуза прямоугольного равнобедренного треугольника в √2 раз больше катета.
Если Вы помните об этом, просто умножьте √2 на √2. Длина диагонали равна двум.
Если Вы об этом не помните, то примените теорему Пифагора: х2 = (√2)2 + (√2)2.
х2 = 2 + 2 = 4. Отсюда так или иначе находим, что диагональ клетки равна двум.
Осталось длину диагонали умножить на три. Средняя линия трапеции равна шести.
Ответ: 6
Если Вам нравится применять формулы, то воспользуемся тем, что средняя линия трапеции равна полусумме оснований.
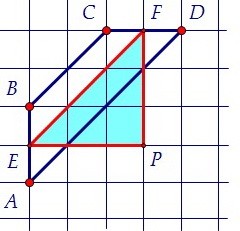 EF2 = (3√2)2 + (3√2)2.
EF2 = 18 + 18 = 36.
EF = 6
EF2 = (3√2)2 + (3√2)2.
EF2 = 18 + 18 = 36.
EF = 6