|
В треугольнике АВС угол В прямой, точка М лежит на стороне АС, причем АМ : МС = √3 : 4. Величина угла АВМ равна 60 градусов, ВМ = 8.
а) Найдите величину угла ВАС.
б) Найдите расстояние между центрами окружностей, описанных вокруг
треугольников ВСМ и ВАМ. 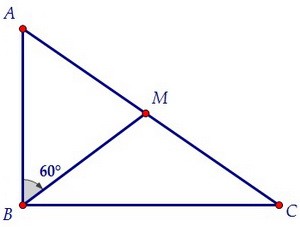 Рассмотрим треугольники АВМ и СВМ найдём отношение их площадей.
Рассмотрим треугольники АВМ и СВМ найдём отношение их площадей.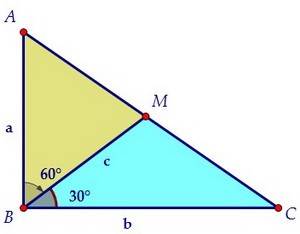 SABM = 0,5·a·c·sin60°
SCBM = 0,5·b·c·sin30°
SABM : SCBM = (a·sin60°) : (b·sin30°) = a√3 : b
С другой стороны, отношение площадей треугольников равно отношению АМ к МС,
так как высоты, проведённые к основаниям АМ и МС, из вершины В, совпадают.
SABM : SCBM = АМ : МС = √3 : 4
Приравнивая найденные отношения, получим отношение b к а, это и есть tgА.
a√3 : b = √3 : 4
a : b = 1 : 4
b : a = 4 = tgА
Заметим, что длину отрезка ВМ мы не использовали! Вот и другой способ:
Проведём из точки М перпендикуляр к АВ и рассмотрим треугольник ВРМ.
SABM = 0,5·a·c·sin60°
SCBM = 0,5·b·c·sin30°
SABM : SCBM = (a·sin60°) : (b·sin30°) = a√3 : b
С другой стороны, отношение площадей треугольников равно отношению АМ к МС,
так как высоты, проведённые к основаниям АМ и МС, из вершины В, совпадают.
SABM : SCBM = АМ : МС = √3 : 4
Приравнивая найденные отношения, получим отношение b к а, это и есть tgА.
a√3 : b = √3 : 4
a : b = 1 : 4
b : a = 4 = tgА
Заметим, что длину отрезка ВМ мы не использовали! Вот и другой способ:
Проведём из точки М перпендикуляр к АВ и рассмотрим треугольник ВРМ.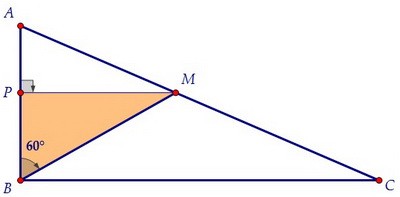 Гипотенуза ВМ равна 8 по условию, катет ВР равен 4 (напротив 30°), РМ = 4√3.
Гипотенуза ВМ равна 8 по условию, катет ВР равен 4 (напротив 30°), РМ = 4√3.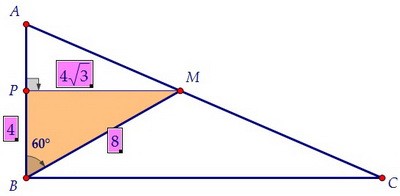 Учитывая теорему Фалеса и условие АМ : МС = √3 : 4, получаем, что АР = √3.
Учитывая теорему Фалеса и условие АМ : МС = √3 : 4, получаем, что АР = √3.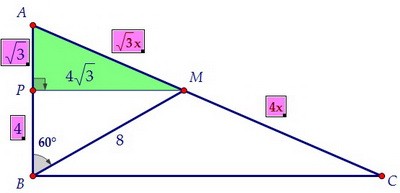 Из треугольника АРМ находим, что tgA = PM : PA = 4√3 : √3 = 4.
Оба центра К и Т описанных около треугольников ВСМ и ВАМ окружностей лежат на серединном перпендикуляре, проведённом к общей стороне ВМ.
Из треугольника АРМ находим, что tgA = PM : PA = 4√3 : √3 = 4.
Оба центра К и Т описанных около треугольников ВСМ и ВАМ окружностей лежат на серединном перпендикуляре, проведённом к общей стороне ВМ.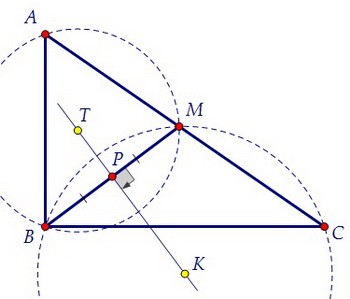 Интересно, что треугольник ТВК подобен треугольнику ВАС по двум углам.
Интересно, что треугольник ТВК подобен треугольнику ВАС по двум углам.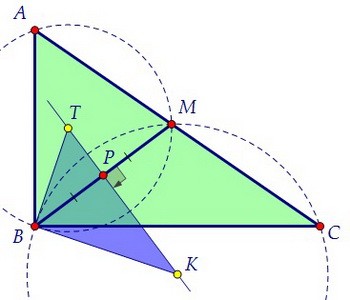 Угол ВАМ вписан в окружность и равен половине дуги, на которую опирается.
Угол ВТР - половина центрального угла ВТМ и равен половине той же дуги.
Угол ВАМ вписан в окружность и равен половине дуги, на которую опирается.
Угол ВТР - половина центрального угла ВТМ и равен половине той же дуги.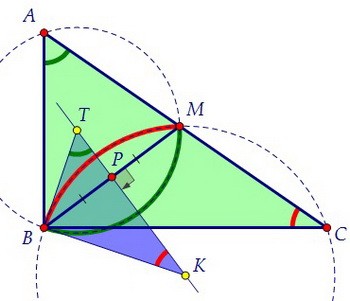 Аналогично равны углы МСВ и РКВ. Это значит, что ∠ТВК = ∠АВС = 90°.
В прямоугольном треугольнике ТВК найдём ТК, если ВР = 4 и tg∠Т = 4
В треугольнике ВТР катет ТР в 4 раза меньше катета ВР, т.е. ТР = 1.
Аналогично равны углы МСВ и РКВ. Это значит, что ∠ТВК = ∠АВС = 90°.
В прямоугольном треугольнике ТВК найдём ТК, если ВР = 4 и tg∠Т = 4
В треугольнике ВТР катет ТР в 4 раза меньше катета ВР, т.е. ТР = 1.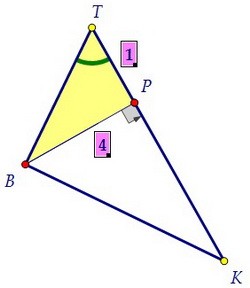 В треугольнике ВКР катет РК в 4 раза больше катета ВР, т.е. РК = 16.
В треугольнике ВКР катет РК в 4 раза больше катета ВР, т.е. РК = 16.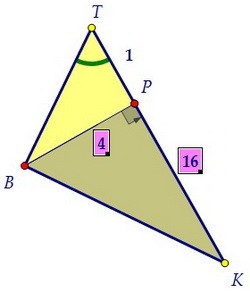 Здесь мы воспользовались тем, что tg∠Т = 4 и tg∠К = 0,25, т.к. ∠Т + ∠К = 90°.
Осталось сложить полученные отрезки, чтобы получить искомое расстояние.
ТК = ТР + РК = 1 + 16 = 17.
Ответ: а) arctg4; б) 17
Здесь мы воспользовались тем, что tg∠Т = 4 и tg∠К = 0,25, т.к. ∠Т + ∠К = 90°.
Осталось сложить полученные отрезки, чтобы получить искомое расстояние.
ТК = ТР + РК = 1 + 16 = 17.
Ответ: а) arctg4; б) 17 Автор: Ольга Себедаш Просмотров: 12941
|

 Рассмотрим треугольники АВМ и СВМ найдём отношение их площадей.
Рассмотрим треугольники АВМ и СВМ найдём отношение их площадей. SABM = 0,5·a·c·sin60°
SCBM = 0,5·b·c·sin30°
SABM : SCBM = (a·sin60°) : (b·sin30°) = a√3 : b
С другой стороны, отношение площадей треугольников равно отношению АМ к МС,
так как высоты, проведённые к основаниям АМ и МС, из вершины В, совпадают.
SABM : SCBM = АМ : МС = √3 : 4
Приравнивая найденные отношения, получим отношение b к а, это и есть tgА.
a√3 : b = √3 : 4
a : b = 1 : 4
b : a = 4 = tgА
Заметим, что длину отрезка ВМ мы не использовали! Вот и другой способ:
Проведём из точки М перпендикуляр к АВ и рассмотрим треугольник ВРМ.
SABM = 0,5·a·c·sin60°
SCBM = 0,5·b·c·sin30°
SABM : SCBM = (a·sin60°) : (b·sin30°) = a√3 : b
С другой стороны, отношение площадей треугольников равно отношению АМ к МС,
так как высоты, проведённые к основаниям АМ и МС, из вершины В, совпадают.
SABM : SCBM = АМ : МС = √3 : 4
Приравнивая найденные отношения, получим отношение b к а, это и есть tgА.
a√3 : b = √3 : 4
a : b = 1 : 4
b : a = 4 = tgА
Заметим, что длину отрезка ВМ мы не использовали! Вот и другой способ:
Проведём из точки М перпендикуляр к АВ и рассмотрим треугольник ВРМ. Гипотенуза ВМ равна 8 по условию, катет ВР равен 4 (напротив 30°), РМ = 4√3.
Гипотенуза ВМ равна 8 по условию, катет ВР равен 4 (напротив 30°), РМ = 4√3. Учитывая теорему Фалеса и условие АМ : МС = √3 : 4, получаем, что АР = √3.
Учитывая теорему Фалеса и условие АМ : МС = √3 : 4, получаем, что АР = √3. Из треугольника АРМ находим, что tgA = PM : PA = 4√3 : √3 = 4.
Оба центра К и Т описанных около треугольников ВСМ и ВАМ окружностей лежат на серединном перпендикуляре, проведённом к общей стороне ВМ.
Из треугольника АРМ находим, что tgA = PM : PA = 4√3 : √3 = 4.
Оба центра К и Т описанных около треугольников ВСМ и ВАМ окружностей лежат на серединном перпендикуляре, проведённом к общей стороне ВМ. Интересно, что треугольник ТВК подобен треугольнику ВАС по двум углам.
Интересно, что треугольник ТВК подобен треугольнику ВАС по двум углам. Угол ВАМ вписан в окружность и равен половине дуги, на которую опирается.
Угол ВТР - половина центрального угла ВТМ и равен половине той же дуги.
Угол ВАМ вписан в окружность и равен половине дуги, на которую опирается.
Угол ВТР - половина центрального угла ВТМ и равен половине той же дуги. Аналогично равны углы МСВ и РКВ. Это значит, что ∠ТВК = ∠АВС = 90°.
В прямоугольном треугольнике ТВК найдём ТК, если ВР = 4 и tg∠Т = 4
В треугольнике ВТР катет ТР в 4 раза меньше катета ВР, т.е. ТР = 1.
Аналогично равны углы МСВ и РКВ. Это значит, что ∠ТВК = ∠АВС = 90°.
В прямоугольном треугольнике ТВК найдём ТК, если ВР = 4 и tg∠Т = 4
В треугольнике ВТР катет ТР в 4 раза меньше катета ВР, т.е. ТР = 1. В треугольнике ВКР катет РК в 4 раза больше катета ВР, т.е. РК = 16.
В треугольнике ВКР катет РК в 4 раза больше катета ВР, т.е. РК = 16. Здесь мы воспользовались тем, что tg∠Т = 4 и tg∠К = 0,25, т.к. ∠Т + ∠К = 90°.
Осталось сложить полученные отрезки, чтобы получить искомое расстояние.
ТК = ТР + РК = 1 + 16 = 17.
Ответ: а) arctg4; б) 17
Здесь мы воспользовались тем, что tg∠Т = 4 и tg∠К = 0,25, т.к. ∠Т + ∠К = 90°.
Осталось сложить полученные отрезки, чтобы получить искомое расстояние.
ТК = ТР + РК = 1 + 16 = 17.
Ответ: а) arctg4; б) 17