Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
14(C2). Площадь сечения пирамиды параллельна скрещивающимся рёбрам (вар. 45)
Комментарии к этой задаче: Комментарий добавил(а): Gleb Почему TK/AS=1/3? Комментарий добавил(а): Валя А почему AS=2AH? Комментарий добавил(а): egetrener Валя, в прямоугольном треугольнике напротив угла 30 градусов лежит катет, в два раза меньший гипотенузы. Комментарий добавил(а): Валентина Очень доступно!!! Комментарий добавил(а): Лана Отличные чертежи и доступное решение, большое спасибо. Комментарий добавил(а): alisa Спасибо! Решала так же, по применяла формулу связи радиуса описаной окружностей и стороны правильного треугольника. Комментарий добавил(а): Anna Почему AS перпендикулярна CB? Комментарий добавил(а): egetrener Анна, в тексте есть ответ на Ваш вопрос. Комментарий добавил(а): ferc Вот за это огромное спасибо! К сожалению, С2 вы показываете редко. Поэтому радуюсь каждой новой задаче! Спасибо! Добавить Ваш комментарий: |

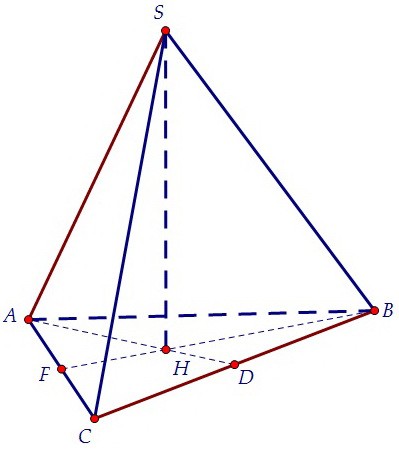 Основание высоты правильной пирамиды - это центр треугольника АВС. Сначала проведём через точку Н отрезок РТ, параллельный ребру ВС. Точки Р и Т принадлежат сечению.
Основание высоты правильной пирамиды - это центр треугольника АВС. Сначала проведём через точку Н отрезок РТ, параллельный ребру ВС. Точки Р и Т принадлежат сечению.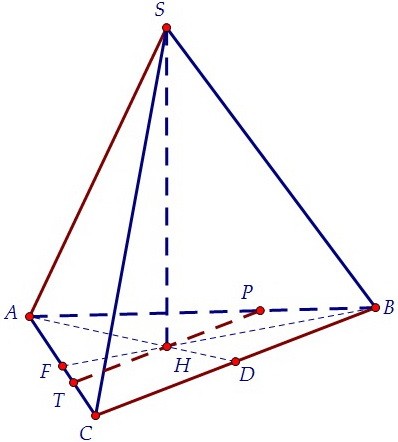 В плоскости грани ACS через точку Т проведём отрезок ТК параллельно ребру AS.
В плоскости грани ACS через точку Т проведём отрезок ТК параллельно ребру AS.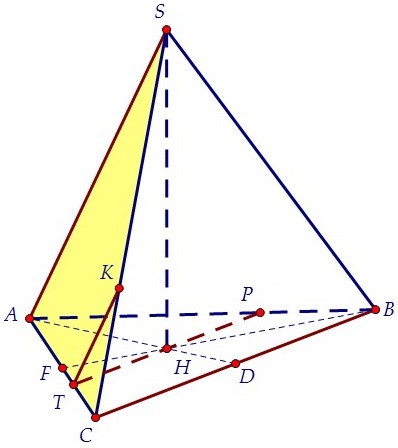 В плоскости грани AВS через точку Р проведём отрезок PL параллельно ребру AS.
В плоскости грани AВS через точку Р проведём отрезок PL параллельно ребру AS.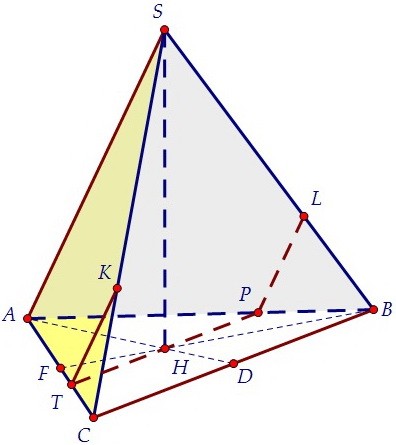 Соединив точки К и L, получим искомое сечение. Докажем, что это прямоугольник.
Соединив точки К и L, получим искомое сечение. Докажем, что это прямоугольник. 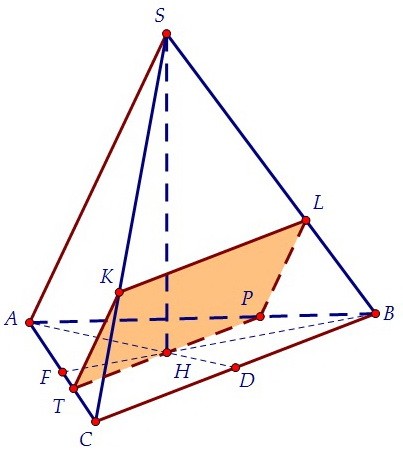 Отрезки ТК и PL не только параллельны (каждый параллелен AS), но и равны.
Отрезки ТК и PL не только параллельны (каждый параллелен AS), но и равны.
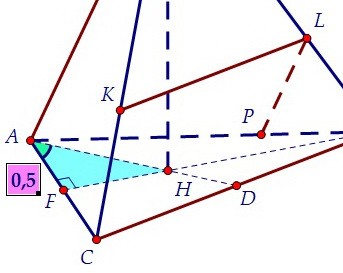
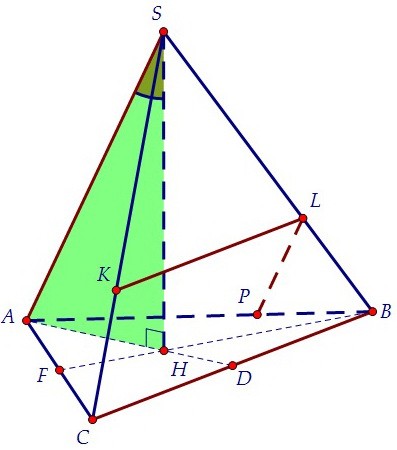 Найти длину отрезка АН, зная сторону основания, можно разными способами.
Лучше обойтись без формул и рассмотреть прямоугольный треугольник АНF.
Найти длину отрезка АН, зная сторону основания, можно разными способами.
Лучше обойтись без формул и рассмотреть прямоугольный треугольник АНF.