Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
7. Количество точек максимума функции по графику производной (вар. 45)
Комментарии к этой задаче: Комментарий добавил(а): Школьник Спасибо большое за пояснения) Комментарий добавил(а): Александр Очень хорошее объяснение. Комментарий добавил(а): Илайчик Что же, надо заучивать Комментарий добавил(а): Олег Спасибо) Комментарий добавил(а): Дмитрий Большое спасибо :) Комментарий добавил(а): Миша Спасибо! Комментарий добавил(а): Катя Большое спасибо.Не могла понять,как эт определяют,а теперь поняла. Комментарий добавил(а): Владимир Спасибо огромное, очень толково и понятно объяснили. Комментарий добавил(а): Ольга Спасибо! Очень понятно нарисовали. Комментарий добавил(а): Людмила а что точка x=18 не является точкой максимума? Комментарий добавил(а): Д Реально помогло и очень понятно Комментарий добавил(а): Лариса спасибо, теперь все понятно! Комментарий добавил(а): ильсия все очень понятно.спасибо Комментарий добавил(а): Комментарий добавил(а): Комментарий добавил(а): Комментарий добавил(а):
Комментарий добавил(а): fynjy Добавить Ваш комментарий: |
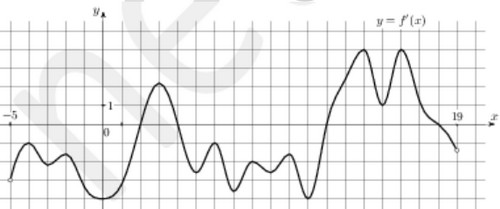
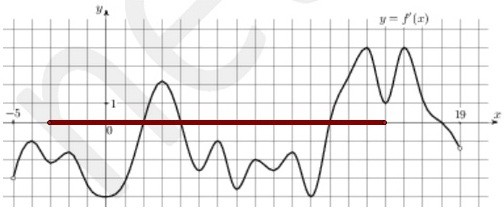Если производная меняет свой знак с "+" на "-", т.е. функция меняет возрастание на убывание
в некоторой точке, то такая точка и есть точка максимума функции. Её-то мы и ищем на графике.
Мы видим три точки, в которых производная равна нулю и меняет свой знак, - точки экстремума.
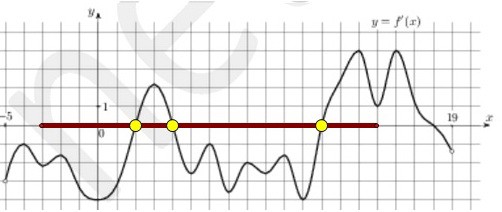И только в одной из них - в точке 4 производная меняет знак с "+" на "-".
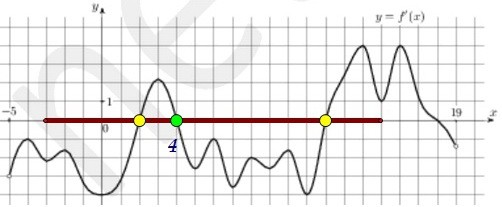Ответ: 1
Для большей уверенности полезно построить простую схему поведения производной.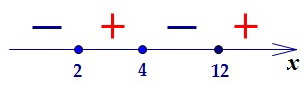
И сделать вывод о поведении функции, а также о количестве точек экстремума.
