|
Найдите наибольшее значение функции на отрезке [19,25; 25,25]
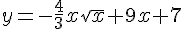
Алгоритм поиска наибольшего (наименьшего) значения функции на отрезке:
1) Ищем производную данной функции.
2) Приравниваем производную нулю и находим критические точки.
3) Отбираем среди них те, которые принадлежат данному отрезку.
4) Вычисляем значения функции в этих точках и на концах отрезка.
5) Сравнивая полученные результаты, делаем выводы и даём ответ.
1) Начнём с производной. Избавимся от корня в первом слагаемом.
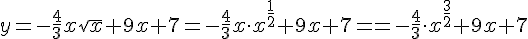 Используем формулы производной степени и производной суммы.
Используем формулы производной степени и производной суммы.
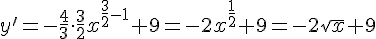 2) Приравниваем производную нулю и найдём критические точки.
2) Приравниваем производную нулю и найдём критические точки.
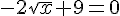
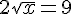
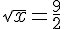
^2)
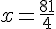 3) Критическая точка 20,25 входит в данный отрезок [19,25; 25,25].
4) Вычислим значения функции в критической точке и на концах отрезка.
3) Критическая точка 20,25 входит в данный отрезок [19,25; 25,25].
4) Вычислим значения функции в критической точке и на концах отрезка.
=y(\frac{81}{4})=-\frac{4}{3}\cdot(\frac{81}{4})\sqrt{\frac{81}{4}}+{9}\cdot(\frac{81}{4})+7={-27}\cdot{\frac{9}{2}}+\frac{27\cdot3\cdot9}{4}+7)
=\frac{27\cdot9}{4}(-2+3)+7=\frac{{27}\cdot{9}+28}{4}=\frac{271}{4})
=y(\frac{77}{4})=-\frac{4}{3}\cdot(\frac{77}{4})\sqrt{\frac{77}{4}}+{9}\cdot(\frac{77}{4})+7=...................)
=y(\frac{101}{4})=-\frac{4}{3}\cdot(\frac{101}{4})\sqrt{\frac{101}{4}}+{9}\cdot(\frac{101}{4})+7=...................) Занятие это скучное, поэтому мы на этом прервёмся и поищем другой путь.
Продолжим исследование функции. Она определена при неотрицательных х.
Найдём знаки производной на интервалах [0; 20,25) и (20,25; +∞).
Занятие это скучное, поэтому мы на этом прервёмся и поищем другой путь.
Продолжим исследование функции. Она определена при неотрицательных х.
Найдём знаки производной на интервалах [0; 20,25) и (20,25; +∞). Если производная положительна, то функция возрастает на этом интервале,
а если производная отрицательна, то функция убывает на этом интервале.
Если производная положительна, то функция возрастает на этом интервале,
а если производная отрицательна, то функция убывает на этом интервале.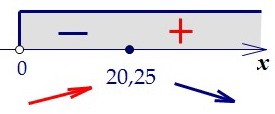 Итак, на [0; 20,25) функция возрастает, на (20,25; +∞) функция убывает.
Это значит, что в точке 20,25 функция достигает наибольшего значения.
А значения функции на концах отрезка, оказывается, можно и не искать.
Итак, на [0; 20,25) функция возрастает, на (20,25; +∞) функция убывает.
Это значит, что в точке 20,25 функция достигает наибольшего значения.
А значения функции на концах отрезка, оказывается, можно и не искать.
=\frac{271}{4}=67,75) Ответ: 67,75
Ответ: 67,75 Автор: Ольга Себедаш Просмотров: 16055
|

 Если производная положительна, то функция возрастает на этом интервале,
а если производная отрицательна, то функция убывает на этом интервале.
Если производная положительна, то функция возрастает на этом интервале,
а если производная отрицательна, то функция убывает на этом интервале. Итак, на [0; 20,25) функция возрастает, на (20,25; +∞) функция убывает.
Это значит, что в точке 20,25 функция достигает наибольшего значения.
А значения функции на концах отрезка, оказывается, можно и не искать.
Итак, на [0; 20,25) функция возрастает, на (20,25; +∞) функция убывает.
Это значит, что в точке 20,25 функция достигает наибольшего значения.
А значения функции на концах отрезка, оказывается, можно и не искать.