Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
ГИА. Модуль Геометрия. Четыре точки лежат на одной окружности (1.10.2013)
Комментарии к этой задаче: Комментарий добавил(а): светлана конечно,красиво,но длинно, трудно и ученикам почти не доступно! Комментарий добавил(а): Тамара Александровна Рыскина Очень грамотно, убедительно и лаконично. Браво ! ! ! Комментарий добавил(а): Елена Опять развлекаются взрослые люди, а задача для кого? Комментарий добавил(а): Ольга Себедаш Елена, задача для думающих людей. Среди учеников таких много. Кто думать не хочет, за такие задачи и не берётся. Зачем? Комментарий добавил(а): Татьяна Васильевна Все понятно. Отлично! Комментарий добавил(а): Майя Красиво! Спасибо Комментарий добавил(а): Лексей Эта задача из ГИА 9 класса. Это очень сложная задача для 9 класса. Кризис образования! Комментарий добавил(а): Денис Сложно. Комментарий добавил(а): Александр Для школьников будет не понятно,а так все нормально Комментарий добавил(а): Алла Ольга, Вы умница! Нигде и никогда не пропускаю ни одного Вашего слова. Комментарий добавил(а): надежда существуют математические классы, таким детям тоже нужно что - то решать. Есть умные дети . Комментарий добавил(а): Валентина Это прекрасно! Красота! Комментарий добавил(а): NathanSip Комментарий добавил(а): Добавить Ваш комментарий: |

 Надо доказать, что четырёхугольник с вершинами в данных точках вписан в окружность.
Надо доказать, что четырёхугольник с вершинами в данных точках вписан в окружность.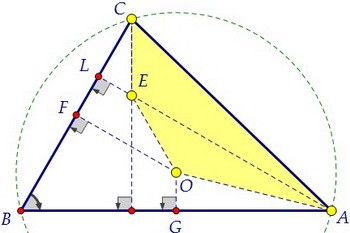 Какие возможны действия? 1) Доказать, например, что сумма углов АСЕ и АОЕ равна 180°.
2) Доказать равенство углов ОАЕ и ЕСО. В этом случае они будут опираться на одну дугу.
Мы выберем третий путь - найдём точку, равноудалённую от всех четырёх жёлтых точек.
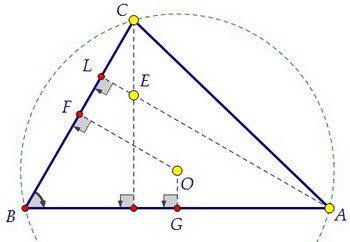
Сначала исследуем данную ситуацию и найдём связь между центром описанной
около треугольника окружности О и точкой пересечения высот треугольника Е.
Какие возможны действия? 1) Доказать, например, что сумма углов АСЕ и АОЕ равна 180°.
2) Доказать равенство углов ОАЕ и ЕСО. В этом случае они будут опираться на одну дугу.
Мы выберем третий путь - найдём точку, равноудалённую от всех четырёх жёлтых точек.
Сначала исследуем данную ситуацию и найдём связь между центром описанной
около треугольника окружности О и точкой пересечения высот треугольника Е.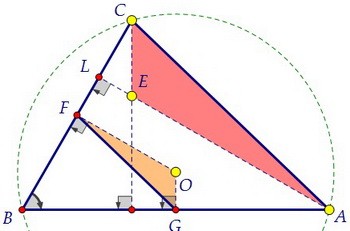 Треугольники FOG и AEC подобны по двум углам, т.к. стороны одного из них
параллельны сторонам другого. Вспомним, что точка О - точка пересечения серединных перпендикуляров к сторонам треугольника, FG - средняя линия.
Коэффициент подобия равен двум, т.к. АС = 2·FG. Значит, CE = 2·OG.
А в прямоугольном треугольнике CEL ∠LCE = 30° и значит, CE = 2·LE.
Треугольники FOG и AEC подобны по двум углам, т.к. стороны одного из них
параллельны сторонам другого. Вспомним, что точка О - точка пересечения серединных перпендикуляров к сторонам треугольника, FG - средняя линия.
Коэффициент подобия равен двум, т.к. АС = 2·FG. Значит, CE = 2·OG.
А в прямоугольном треугольнике CEL ∠LCE = 30° и значит, CE = 2·LE.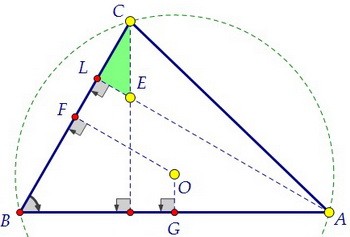 Из двух последних равенств делаем замечательный вывод о том, что OG = LE.
Из двух последних равенств делаем замечательный вывод о том, что OG = LE.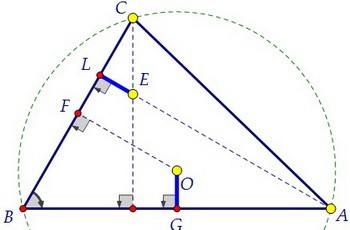 В прямоугольном треугольнике АВL ∠BAL = 30° и BL = 0,5·AB. Значит, BL = BG.
В прямоугольном треугольнике АВL ∠BAL = 30° и BL = 0,5·AB. Значит, BL = BG.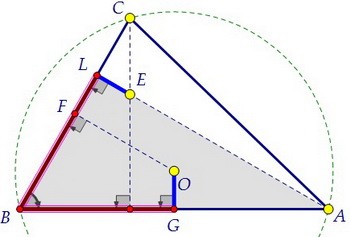 Прямоугольные треугольники ВLЕ и BGO равны по двум катетам. Значит, ВЕ = ВО.
Прямоугольные треугольники ВLЕ и BGO равны по двум катетам. Значит, ВЕ = ВО.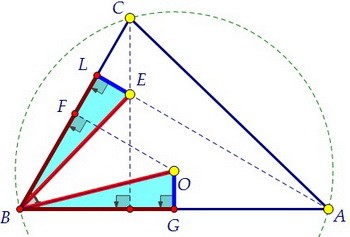 Треугольник ОВЕ равнобедренный, биссектриса ВТ угла ОВЕ является и серединным перпендикуляром к отрезку ОЕ, а также (очевидно) биссектрисой угла АВС.
Треугольник ОВЕ равнобедренный, биссектриса ВТ угла ОВЕ является и серединным перпендикуляром к отрезку ОЕ, а также (очевидно) биссектрисой угла АВС.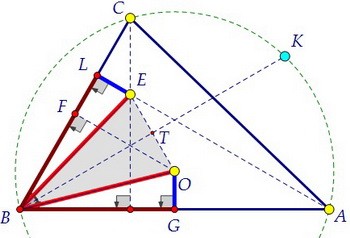 Точка К пересечения биссектрисы и окружности и есть точка, равноудаленная от четырёх жёлтых точек С, А, О, Е. Осталось этот факт доказать.
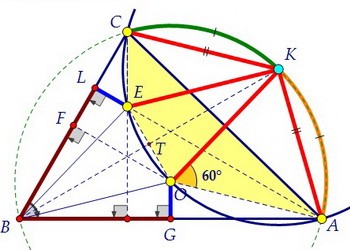
Точка К пересечения биссектрисы и окружности и есть точка, равноудаленная от четырёх жёлтых точек С, А, О, Е. Осталось этот факт доказать.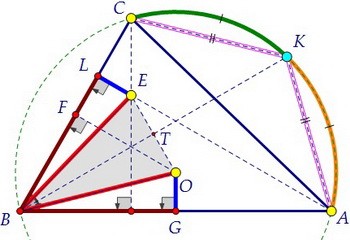 Т.к. ВК - биссектриса, то точка К делит дугу АС пополам, следовательно, СК = АК.
∠КОА = 2·∠КВА = 60°, ОК = ОА = R. Значит, треугольник ОКА равносторонний.
Т.к. ВК - биссектриса, то точка К делит дугу АС пополам, следовательно, СК = АК.
∠КОА = 2·∠КВА = 60°, ОК = ОА = R. Значит, треугольник ОКА равносторонний.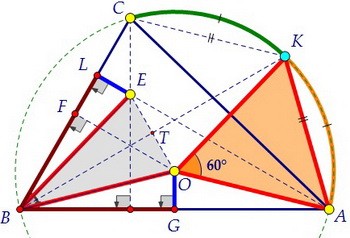 Легко увидеть, что КЕ = КО. Из всех равных красных отрезков оставим только основные.
Легко увидеть, что КЕ = КО. Из всех равных красных отрезков оставим только основные.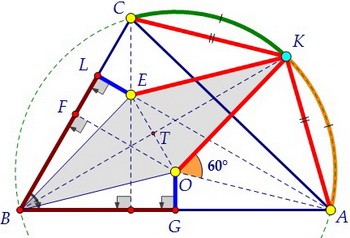 Найден центр окружности. описанной около четырёхугольника САОЕ. Утверждение доказано.
Найден центр окружности. описанной около четырёхугольника САОЕ. Утверждение доказано.