Егэ-тренер. Подготовка 2019-2020 Тренинги в прямом эфире для учителей и учеников |
|
ГИА. Модуль "Геометрия". Окружности касаются внешним образом
Комментарии к этой задаче: Комментарий добавил(а): Кака Девятиклассики знают теорему косинусов Не надо врать! Комментарий добавил(а): Светлана Прекрасное решение! Спасибо за пошаговые рассуждения и рисунки, но девятиклассники еще не знают теорему косинусов, а без теоремы решение более объемное. Рановато дали такую задачу! Комментарий добавил(а): Флюра А еще девятые классы не изучали прогрессию и решение квадратичных неравенств. Комментарий добавил(а): нина Задача №25 больше подходит под №26,а № 26 дали рано. Комментарий добавил(а): Елена Сложность заданий по геометрии 2 ч. выходит за рамки программы и факультатива.Как учителю извернуться, чтобы оправдать свою зарплату(?),ведь с его мнением не желают считаться господа составители тестов. Им решение-забава, а учителю ??? Комментарий добавил(а): Ольга Себедаш Елена, мне не кажется, что задача выходит за рамки школьной программы. Она просто для думающих детей. Совершенно необязательно решать её каждому. Комментарий добавил(а): Александр в 9-м классе теорема косинусов есть в школьной программе. Комментарий добавил(а): Виолета Не все девятиклассники знают эту теорему, тут уж смотря какая программа, не все углубленнки изучают ее в одно и тоже время-кто-то раньше, кто-то позже Комментарий добавил(а): Дарья Как дальше решать без теоремы косинусов? Комментарий добавил(а): илья девятиклассники знают теорему косинусов! Комментарий добавил(а): Глеб Даже большинство людей закончивших 8 класс знают теорему косинусов Комментарий добавил(а): Глеб Процентов 96 примерно Комментарий добавил(а): ИринА Огромное спасибо! Отличное обьяснение! А теорему косинусов в 9 классе не знает только тот, кто не учится. Эта теорема не из углубленного курса геометрии. Добавить Ваш комментарий: |

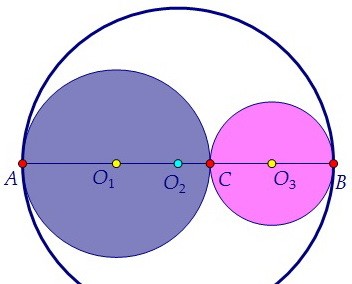 Попробуем сделать чертёж по-другому. Возможна ли такая ситуация, как на рисунке?
Попробуем сделать чертёж по-другому. Возможна ли такая ситуация, как на рисунке?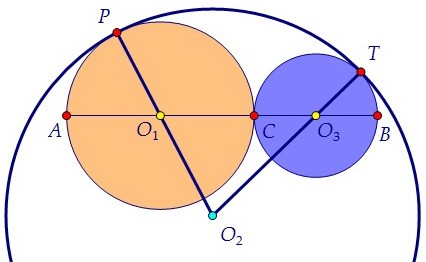 Если окружности касаются друг друга внутренним образом, то расстояние между центрами
равно разности их радиусов, т.е. R2 - R1 = O1O2. Значит, O1O2 = 14 - 7 = 7, т.е. O1O2 = R1.
Если расстояние от точки до центра окружности равно радиусу, то она лежит на окружности.
Если окружности касаются друг друга внутренним образом, то расстояние между центрами
равно разности их радиусов, т.е. R2 - R1 = O1O2. Значит, O1O2 = 14 - 7 = 7, т.е. O1O2 = R1.
Если расстояние от точки до центра окружности равно радиусу, то она лежит на окружности.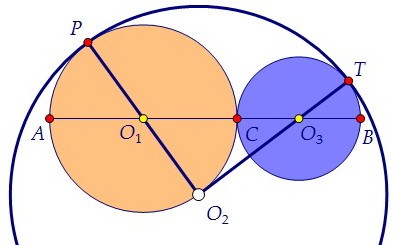 Итак, чертёж сделан теперь хорошо. Угол O1O2O3 найдём из треугольника O1O2O3.
Итак, чертёж сделан теперь хорошо. Угол O1O2O3 найдём из треугольника O1O2O3.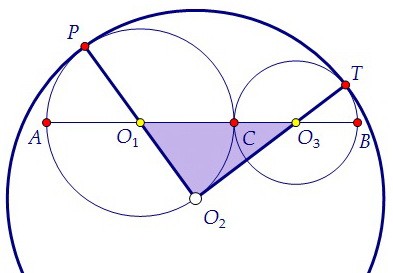 Для этого найдём все три его стороны: O1O2 = 14 - 7 = 7, O1O3 = 7 + 6 = 13, O2O3 = 14 - 6 = 8.
Для этого найдём все три его стороны: O1O2 = 14 - 7 = 7, O1O3 = 7 + 6 = 13, O2O3 = 14 - 6 = 8.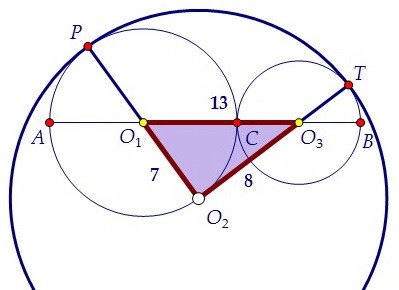 Осталось применить теорему косинусов для стороны O1O3:
Осталось применить теорему косинусов для стороны O1O3: