Егэ-тренер. Подготовка 2014-2015 Тренинги в прямом эфире для учителей и учеников |
|
ГИА. Модуль "Геометрия". В трапеции диагонали перпендикулярны
Комментарии к этой задаче: Комментарий добавил(а): Лилия Очень красивое решение. Комментарий добавил(а): Галина Михайловна Красивое решение Комментарий добавил(а): Игорь Красивое решение, не буду оригинальничать) Комментарий добавил(а): Елена красивое решение, с этим не поспоришь. Комментарий добавил(а): нв спасибо, всё понятно Комментарий добавил(а): Яна красивое решение, прекрасное объяснение. Комментарий добавил(а): наташа спасибо замечательное пояснение Комментарий добавил(а): Татьяна Можно проще: Так как треугольники АОD и BOC равнобедренные, то высота трапеции, проведенная через точку О(пересечение диагоналей) будет состоять из медиан этих треугольников. Но медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы. Значит высота трапеции равна полусумме оснований, то есть равна средней линии трапеции. Комментарий добавил(а): Яна спасибо большое) очень хорошая решения) и все понятно) Комментарий добавил(а): Раиса Красивое решение и понятное Комментарий добавил(а): Катя Понятное и красивое решение) не поспоришь Комментарий добавил(а): Мадина Просто супер Комментарий добавил(а): Наталья Анатольевна большое спасибо Комментарий добавил(а): Анастасия Огромное спасибо! Никак не могла вникнуть в суть задачи, а после вашего объяснения все на свои места встало!! Комментарий добавил(а): Галина спасибо,задача решена красиво и понятно. Комментарий добавил(а): Алиса А ещё есть свойство: если в равнобедренной трапеции диагонали перпендикулярны, то высота, проведённая к большему основании, равна средней линии. В данном случае высота уже дана, так что задача в одно действие Комментарий добавил(а): Ольга Себедаш Алиса, так любую задачу можно обозвать свойством)) Данная задача и дана для того, чтобы это свойство простое ученик доказал. В этом и суть. Комментарий добавил(а): алик большое спасибо Комментарий добавил(а): Deweydooms If you have a desire to learn how to earn from $ 500 per day and work only for yourself, then write to us at email: admin@makemoneyonline.universalxyzdom.xyz Добавить Ваш комментарий: |
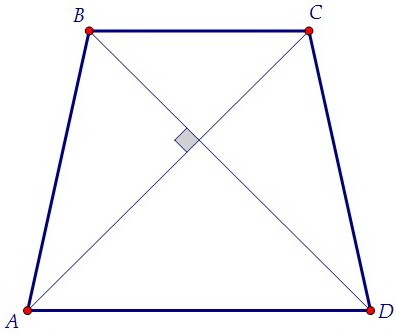Проведём высоту, длина которой дана по условию, сначала из вершины тупого угла (BH),
затем через точку пересечения диагоналей. Высота EF является осью симметрии трапеции.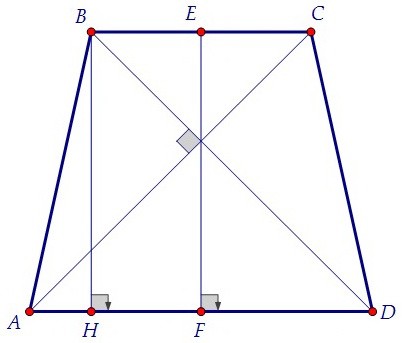
Средняя линия трапеции равна полусумме её оснований. Рисовать мы её не будем, но вычислим:
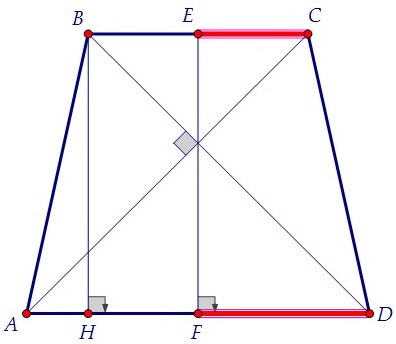Учтём, что ЕС = ВЕ и ВЕ = HF. Получим ЕС = HF. Продолжим верхнее равенство:
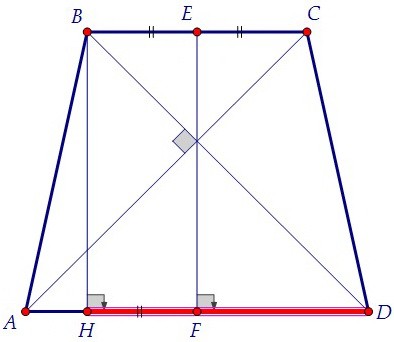Задачу переформулируем так - зная высоту трапеции ВН, найти длину отрезка HD.
Интуиция подсказывает наверняка, что треугольник BHD равнобедренный и HD = 16.
Докажем это. Треугольник АОD прямоугольный равнобедренный, значит, ∠ODA = 45°.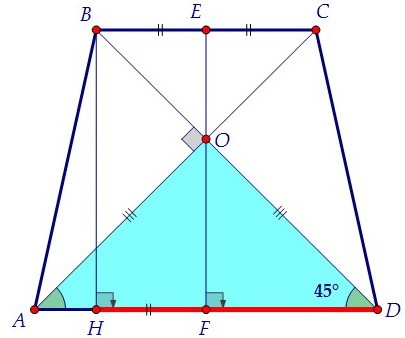
А в прямоугольном треугольнике BHD второй острый угол тоже равен 45°. Значит, и он равнобедренный.
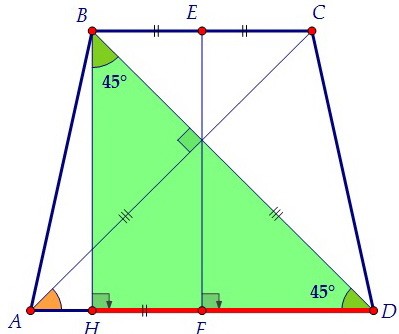В равнобедренном треугольнике боковые стороны равны и HD = BH = 16.
Ответ: 16
