Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В трапеции ABCD с боковыми сторонами AB = 8 и CD = 5 биссектриса угла В пересекает
биссектрисы углов А и С в точках M и N соответственно, а биссектриса угла D пересекает
те же две биссектрисы в точках L и К, причем, точка L лежит на основании ВС.
а)  Докажите, что прямая МК проходит через середину стороны АВ 
б)  Найти отношение KL : MN, если LM : KN = 4 : 7.

Пересечём все биссектрисы трапеции. Первый чертёж выйдет, скорее всего, таким: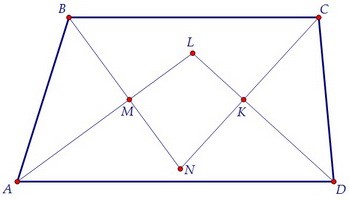



Так точка L должна оказаться на основании ВС, поднимем немного основание AD.



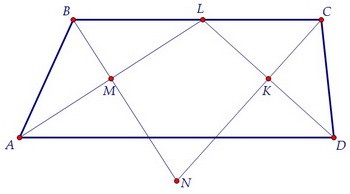Исследуем полученную конструкцию. ∠1 = ∠2 по свойству параллельных прямых, ∠1 = ∠3
по определению биссектрисы. Следовательно, ∠3 = ∠2, и треугольник ABL равнобедренный.



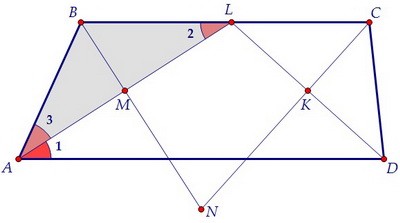В равнобедренном треугольнике биссектриса ВМ является высотой и медианой. АМ = МL.



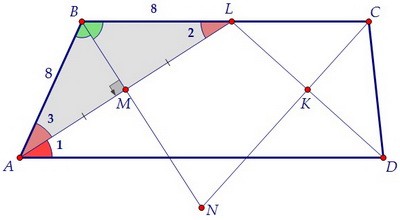Для доказательства пункта а) докажем, что точки М и К равноудалены от оснований ВС и AD.
Проведём через точку М перпендикуляр к основаниям и рассмотрим треугольники АМН и LMS.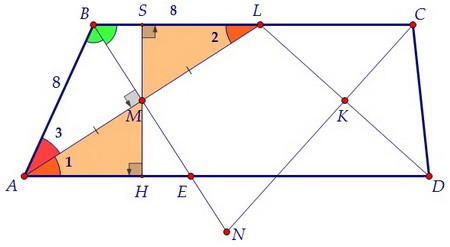



Эти прямоугольные треугольники равны по гипотенузе и острому углу. Значит, MS = MH.
Аналогично КР = QK, значит, MК || SP || HQ, MК = SP = HQ (MSPК - прямоугольник).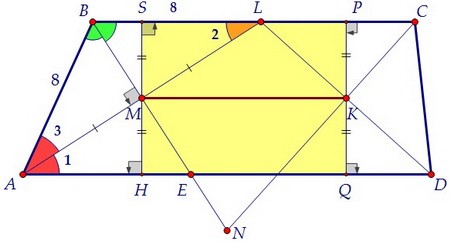



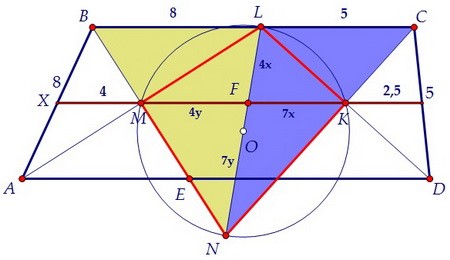
Продлим MК до пересечения с боковой стороной АВ в точке Х.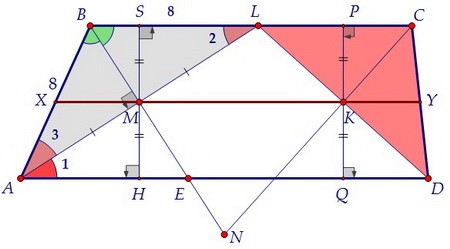



По теореме Фалеса точка Х поделит АВ пополам, т.к. MХ || BL и AM = ML.
Доказав пункт а) мы заодно показали, что LC = CD = 5, ХМ = 4, KY = 2,5.
Около четырёхугольника MLKN опишем окружность, середина гипотенузы
LN обоих прямоугольных треугольников MLN и KLN является её центром.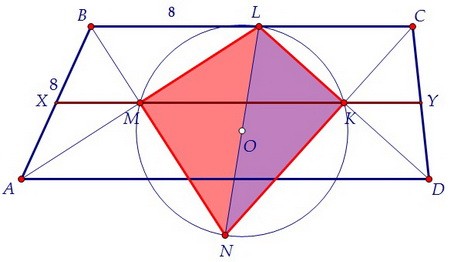



Треугольники MLF и NKF подобны по двум углам (вписанные опираются на одну дугу).



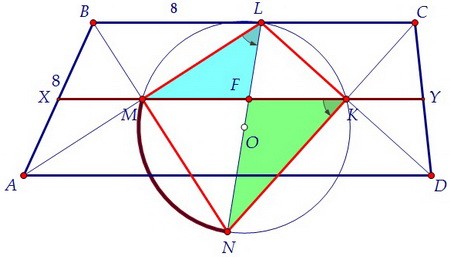Коэффициент подобия равен 4/7, т.к. LM : KN = 4 : 7 по условию задачи.
LF : KF = MF : NF = LM : KN = 4 : 7. Введём переменные x и y, тогда:



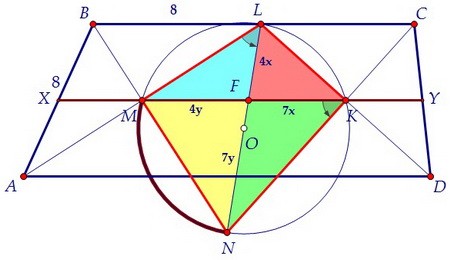Треугольники LFK и MFN подобны по двум углам (или по двум сторонам и углу
между ними), FL : FM = FM : FN = x : y, т.е. коэффициент подобия равен х/y.
Найдя этот коэффициент, найдём автоматически и отношение KL : MN = x : y.
Используя подобие треугольников MNF и BNL, а также KNF и CNL, получим:









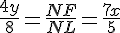
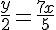
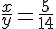Ответ: 5 : 14

Автор: Ольга Себедаш             Просмотров: 13856