Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

На рисунке изображен график производной y = f '(x) функции f(x), определенной на интервале (‐1;16).
Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

Поведение функции зависит от знака производной. Если производная на интервале положительна,
то функция на этом интервале возрастает. Если производная отрицательна, то функция убывает.



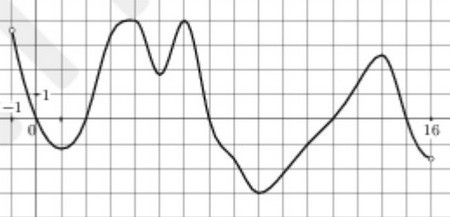
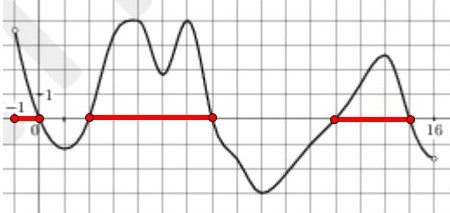Поэтому прежде всего на графике производной надо обратить внимание на участки,
расположенные выше оси ОХ, именно на этих интервалах производная положительна,
а значит, функция возрастает. Таких интервалов на рисунке три, их длины 1, 3 и 5.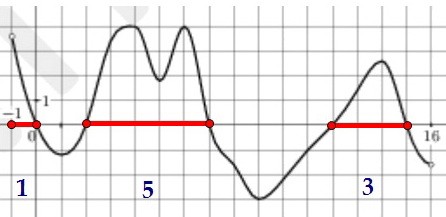



Наибольшая из этих длин, очевидно, 5.

Ответ: 5

Автор: Ольга Себедаш             Просмотров: 72757