Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

В правильной четырёхугольной пирамиде SABCD точка O - центр основания,
S - вершина, SO = 20, SD = 25. Найдите длину отрезка BD.

В правильной четырёхугольной пирамиде основанием является квадрат.
Вершина такой пирамиды проектируется в центр квадрата, т.е. в точку
пересечения диагоналей. Диагонали квадрата делятся этой точкой
пополам. Поэтому точка О - середина BD и SO - высота пирамиды.



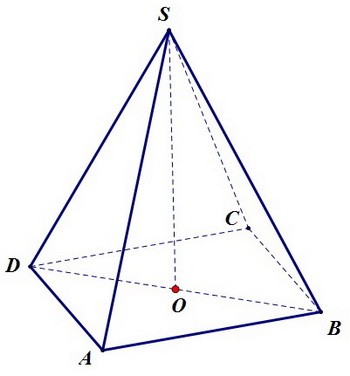
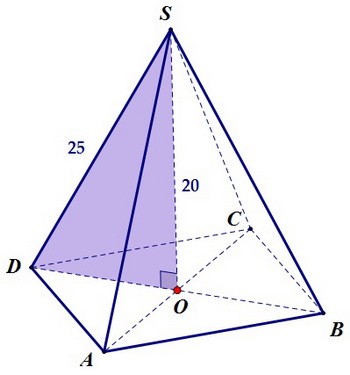Высота SO перпендикулярна основанию, а значит, и прямой BD основания.
Треугольник DSO прямоугольный с катетом SO = 20 и гипотенузой SD = 25.
Осталось применить теорему Пифагора, чтобы найти второй катет.
Квадрат гипотенузы равен сумме квадратов катетов:













Половина диагонали равна 15, значит, вся диагональ равна 30.

Ответ: 30

Замечу, что теорему Пифагора можно было применить для треугольника
подобного данному с коэффициентом подобия, равным 5.



По гипотенузе 5 и катету 4 легко найти второй катет 3, а затем умножить его на 5.

Автор: Ольга Себедаш             Просмотров: 46361