Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

На рисунке изображен график y = f'(x) производной функции f(x), определённой на интервале (-3; 8).
В какой точке отрезка [-2; 3] функция f(x) принимает наименьшее значение?

Отметим отрезок [-2; 3] на оси ох. Как ведёт себя на отрезке производная?
Она имеет свои максимумы, минимумы и всевозможные изгибы, но это неважно.



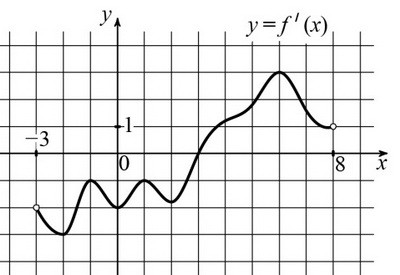
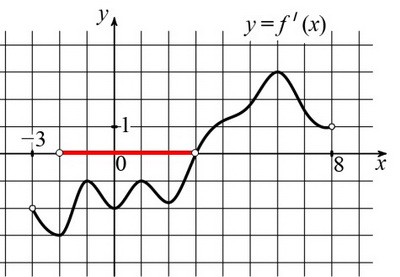Важно лишь то, что производная на интервале (-2; 3) отрицательна. Поведение функции
зависит от знака производной. Если производная отрицательна, то функция убывает.



Так как функция на отрезке [-2; 3] монотонно убывает, то своё наименьшее значение
она достигает в правом конце отрезка, т.е. в точке 3.

Ответ: 3

Автор: Ольга Себедаш             Просмотров: 76659