Егэ-тренер. Подготовка 2019-2020
Тренинги в прямом эфире для учителей и учеников

Периметр треугольника ABC равен 6. Найдите периметр треугольника FDE,
вершинами которого являются середины сторон треугольника ABC.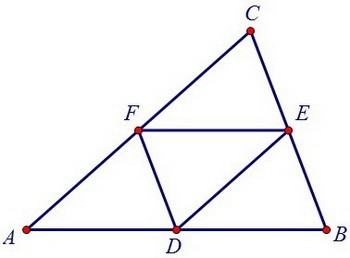

Стороны маленького треугольника являются средними линиями большого. Средняя линия
треугольника в два раза меньше его основания. Обозначим маленькие стороны x, y и z.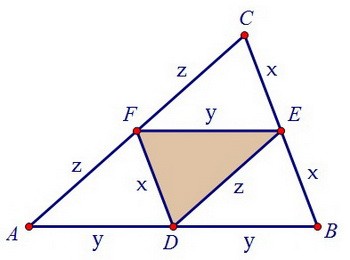



Тогда стороны большого треугольника равны 2x, 2y и 2z. Периметр - это сумма всех сторон.
P_ABC = 2x + 2y + 2z. По условию задачи эта сумма равна шести, то есть 2x + 2y + 2z = 6.
Поделим это равенство на два и получим: x + y + z = 3. А это означает, что P_DEF = 3.

Ответ: 3

Решим задачу и с помощью подобия. Докажем подобие треугольников ABC и DEF.
Четырёхугольник AFED - параллелограмм по определению параллелограмма, т.к. его
противоположные стороны попарно параллельны (работает свойство средней линии).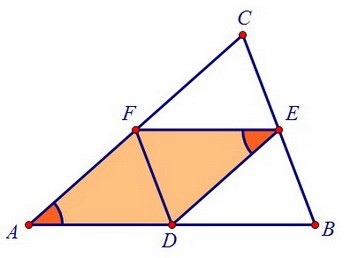



А у параллелограмма противоположные углы равны по свойству параллелограмма.
Получаем, что ∠FAD = ∠FED. И аналогично имеем: ∠DВЕ = ∠DFE и ∠FСЕ = ∠FDЕ.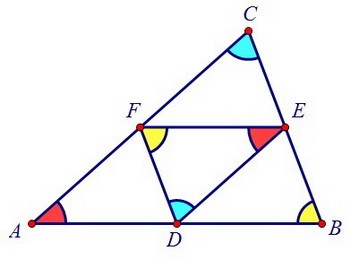



Треугольники подобны по двум углам, а коэффициент подобия равен двум. Все
соответствующие линейные размеры отличаются в два раза. Значит, и периметр
треугольника DEF в два раза меньше периметра треугольника ABC.

Замени теперь в условии слова "периметр" на слова "площадь" и реши новую задачу:

Площадь треугольника ABC равен 6. Найдите площадь треугольника FDE,
вершинами которого являются середины сторон треугольника ABC.

Автор: Ольга Себедаш             Просмотров: 43197